How to solve cos equations. Equation cos x = a

Zakharova Lyudmila Vladimirovna
MBOU "Secondary school No. 59" of Barnaul
mathematic teacher [email protected]

№1 The simplest trigonometric equations

Target: 1. Derive formulas for solutions of the simplest trigonometric equations of the form sinx =a, cosx=a, tgx=a, ctgx=a;

2. Learn to solve simple trigonometric equations using formulas.

Equipment: 1) Tables with graphs of trigonometric functions y= sinx, y=cosx, y=tgx, y=ctgx; 2) Table of values of inverse trigonometric functions; 3) Summary table of formulas for solving simple trigonometric equations.

Lecture lesson plan:

1 .Derivation of formulas for the roots of the equation

a) sinx =a,

b) cosx= a,

c) tgx= a,

d) ctgx= A.

2 . Oral frontal work to consolidate the received formulas.

3 . Written work to consolidate the studied material

During the classes.

In algebra, geometry, physics and other subjects, we are faced with a variety of problems, the solution of which involves solving equations. We have studied the properties of trigonometric functions, so it is natural to turn to equations in which the unknown is contained under the function sign

Definition: Equations of the form sinx = a , cosx= a , tgx= a , ctgx= A are called the simplest trigonometric equations.

It is very important to learn how to solve the simplest trigonometric equations, since all methods and techniques for solving any trigonometric equations consist in reducing them to the simplest.

Let's start by deriving formulas that “actively” work when solving trigonometric equations.

1.Equations of the form sinx = a.

Let's solve the equation sinx = a graphically. To do this, in one coordinate system we will construct graphs of the functions y=sinx and y= A.

1) If A> 1 and A sin x= A has no solutions, since the straight line and the sine wave do not have common points.

2) If -1a a crosses the sine wave infinitely many times. This means that the equation sinx= a has infinitely many solutions.

Since the period of sine is 2 , then to solve the equation sinx= a it is enough to find all solutions on any segment of length 2.

Solving the equation on [-/2; /2] by definition of arcsine x= arcsin a, and on x=-arcsin a. Taking into account the periodicity of the function у=sinx, we obtain the following expressions

x = -arcsin a+2n, n Z.

Both series of solutions can be combined

X = (-1) n arcsin a+n, nZ.

In the following three cases, they prefer to use simpler relations rather than a general formula:

If A=-1, then sin x =-1, x=-/2+2n

If A=1, then sin x =1, x =/2+2n

If a= 0, then sin x =0. x = n,

Example: Solve an equation sinx =1/2.

Let's create formulas for solutions x=arcsin 1/2+ 2n

X= - arcsin a+2n

Let's calculate the value arcsin1/2. Let's substitute the found value into the solution formulas

x=5/6+2 n

or according to the general formula

X= (-1) n arcsin 1/2+n,

X= (-1) n /6+n,

2. Equations of the form cosx= a.

Let's solve the equation cosx= a also graphically, by plotting the functions y= cosx and y= A.

1) If a 1, then the equation cosx= a has no solutions, since the graphs do not have common points.

2) If -1 a cosx= a has an infinite number of solutions.

We will find all the solutions cosx= a on an interval of length 2 since the period of the cosine is 2.

By the definition of arc cosine, the solution to the equation will be x= arcos a. Considering the parity of the cosine function, the solution to the equation on [-;0] will be x=-arcos a.

Thus, solving the equation cosx= a x= + arcos a+ 2 n,

In three cases, we will not use the general formula, but simpler relations:

If A=-1, then cosx =-1, x =-/2+2n

If A=1, then cosx =1, x = 2n,

If a=0, then cosx=0. x =/2+n

Example: Solve an equation cos x =1/2,

Let's create formulas for solutions x=arccos 1/2+ 2n

Let's calculate the value arccos1/2.

Let's substitute the found value into the solution formulas

X= + /3+ 2n, nZ.

Equations of the form tgx= a.

Since the period of the tangent is equal, then in order to find all solutions to the equation tgx= a, it is enough to find all solutions on any interval of length . By definition of arctangent, the solution to the equation on (-/2; /2) is arctan a. Taking into account the period of the function, all solutions to the equation can be written in the form

x= arctan a+ n, nZ.

Example: Solve the equation tan x = 3/3

Let's create a formula for solving x= arctan 3/3 +n, nZ.

Let's calculate the arctangent value arctan 3/3= /6, then

X=/6+ n, nZ.

Derivation of the formula for solving the equation With tgx= a can be provided to students.

Example.

Solve the equation ctg x = 1.

x = arcсtg 1 + n, nZ,

X = /4 + n, nZ.

As a result of the material studied, students can fill out the table:

"Solving trigonometric equations."

the equation

Exercises to consolidate the studied material.

(Oral) Which of the written equations can be solved using the formulas:

a) x= (-1) n arcsin a+n, nZ;

b) x= + arcos a+ 2 n?

cos x = 2/2, tan x= 1, sin x = 1/3, cos x = 3/3, sin x = -1/2, cos x= 2/3, sin x = 3, cos x = 2 .

Which of the following equations have no solutions?

Solve the equations:

a) sin x = 0; e) sin x = 2/2; h) sin x = 2;

b) cos x = 2/2; e) cos x = -1/2; i) cos x = 1;

d) tan x = 3; g) cot x = -1; j) tan x = 1/ 3.

3. Solve the equations:

a) sin 3x = 0; e) 2cos x = 1;

b) cos x/2 =1/2; e) 3 tg 3x =1;

d) sin x/4 = 1; g) 2cos(2x+ /5) = 3.

When solving these equations, it is useful to write down the rules for solving equations of the form sin V x = a, And With sin V x = a, | a|1.

Sin V x = a, |a|1.

V x = (-1) n arcsin a+n, nZ,

x= (-1) n 1/ V arcsin a+n/ V, nZ.

Summing up the lesson:

Today in class we derived formulas for solving simple trigonometric equations.

We looked at examples of solving simple trigonometric equations.

We filled out the table that we will use to solve the equations.

Homework.

№2 Solving trigonometric equations

Target: Study methods for solving trigonometric equations: 1) reducible to quadratic; 2) reducible to homogeneous trigonometric equations.

To develop students' powers of observation when using various methods of solving trigonometric equations.

Frontal work with students.

What are the formulas for the roots of trigonometric equations? cos x= a, sin x= a, tgx = a, ctg x = a.

Solve the equations (orally):

cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1.5, sin x=0.

Find the errors and think about the reasons for the errors.

cos x=1/2, x= + /6+2k,k Z.

sin x= 3/2, x= /3+k, kZ.

tgx = /4, x=1+ k, kZ.

2. Studying new material.

This lesson will cover some of the most common methods for solving trigonometric equations.

Trigonometric equations reduced to quadratic.

This class can include equations that include one function (sine or cosine) or two functions of the same argument, but one of them is reduced to the second using basic trigonometric identities.

For example, if cosх enters the equation in even powers, then we replace it with 1-sin 2 x, if sin 2 x, then we replace it with 1-cos 2 x.

Example.

Solve equation: 8 sin 2 x - 6sin x -5 =0.

Solution: Let's denote sin x=t, then 8t 2 - 6t – 5=0,

D= 196,

T 1 = -1/2, t 2 = -5/4.

Let's perform the reverse substitution and solve the following equations.

X=(-1) k+1 /6+ k, kZ.

Since -5/4>1, the equation has no roots.

Answer: x=(-1) k+1 /6+ k, kZ.

Solving consolidation exercises.

Solve the equation:

1) 2sin 2 x+ 3cos x = 0;

2) 5sin 2 x+ 6cos x -6 = 0;

3) 2sin 2 x+ 3cos 2 x = -2sin x;

4) 3 tg 2 x +2 tgx-1=0.

Homogeneous trigonometric equations.

Definition: 1) Equation of the forma sinx + b cosx=0, (a=0, b=0) is called a homogeneous equation of the first degree with respect to sin x and cos x.

This equation is solved by dividing both sides by cosx 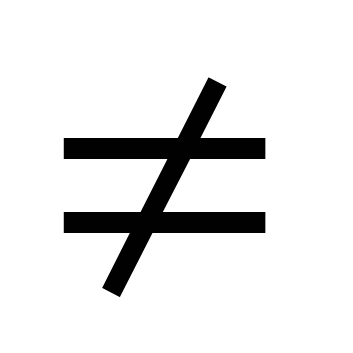0. The result is the equation atgx+ b=0.

2) Equation of the forma sin 2 x + b sinx cosx + c cos 2 x =0 is called a homogeneous equation of the second degree, where a, b, c are any numbers.

If a = 0, then we solve the equation by dividing both sides by cos 2 x 0. As a result, we obtain the equation atg 2 x+ btgx+с =0.

Comment: Equation of the forma sin mx + b cos mx=0 or

a sin 2 mx + b sin mx cos mx + c cos 2 mx =0 are also homogeneous. To solve them, both sides of the equation are divided by cos mx=0 or cos 2 mx=0

3) Various equations that are not originally homogeneous equations can be reduced to homogeneous equations. For example,sin 2 mx + b sin mx cos mx + c cos 2 mx = d, And a sinx + b cosx= d. To solve these equations, you need to multiply the right-hand side by "trigonometric unit" those. on sin 2 x + cos 2 x and perform mathematical transformations.

Exercises to consolidate the studied material:

1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;

2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;

3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;

4) sin 2 x -3 sinx cosx +2 cos 2 x =0

3. Summing up the lesson. Homework.

In this lesson, depending on the preparedness of the group, you can consider solving equations of the form a sin mx +b cos mx=c, where a, b, c are not equal to zero at the same time.

Strengthening exercises:

1. 3sin x + cos x=2;

2. 3sin 2x + cos 2x= 2;

3. sin x/3 + cos x/3=1;

4. 12 sin x +5 cos x+13=0.

№ 3 Solving trigonometric equations

Target: 1) Study the method of solving trigonometric equations by factorization; learn to solve trigonometric equations using various trigonometric formulas;

2) Check: students’ knowledge of formulas for solving simple trigonometric equations; ability to solve simple trigonometric equations.

Lesson plan:

Checking homework.

Mathematical dictation.

Learning new material.

Independent work.

Summing up the lesson. Homework.

Progress of the lesson:

Checking homework (solutions to trigonometric equations are briefly written on the board).

Mathematical dictation.

IN 1

1. What equations are called the simplest trigonometric equations?

2. What is the name of the equation of the forma sinx + b cosx=0? Indicate a way to solve it.

3.Write down the formula for the roots of the equation tgx = a(ctg x= a).

4. Write down the formulas for the roots of equations of the form cosx= a, Where A=1, A=0, A=-1.

5. Write down the general formula for the roots of the equation sin x= a, | a|

6. How equations of the form are solveda cosx= b, | b|

AT 2

1. Write down the formulas for the roots of the equations cosx= a,| a|

2. Write down the general formula for the roots of the equation

= a, | a|

3. What are equations of the form called? sin x= a, tgx = a, sin x= a?

4.Write down the formulas for the roots of the equation sin x= a, If A=1, A=0, A=-1.

5. How equations of the form are solved sin a x= b, | b|

6. What equations are called homogeneous equations of the second degree? How are they resolved?

Learning new material.

Factorization method.

One of the most commonly used methods for solving trigonometric equations is the factorization method.

If the equation f(x) =0 can be represented as f 1 (x) f 2 (x) =0, then the problem is reduced to solving two equations f 1 (x) = 0, f 2 (x) = 0.

(With students it is useful to remember the rule “ The product of factors is equal to zero if at least one of the factors is equal to zero, and the others make sense»)

Consolidation of the studied material through solving equations of varying complexity.

(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(self)

3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;

5) sin 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2 ways)

7) cosx+ cos3x=0; 8) sin 3x= sin 17x;

9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x

11) sin x cos5x = sin 9x cos3x sin 2x sin 2x

12) 3 cosx sin x+ cos 2 x=0(self)

13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.

Independent work.

Option-1 Option-2

1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;

2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;

3) 5 sin 2 x+ sin x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5;

4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;

5) sin x+cosx=1. 5) sin x+cosx=2.

8. Summing up the lesson. Homework.

Lesson type: setting a learning task.

Lesson objectives:

Educational: systematize students’ knowledge about methods for solving simple trigonometric equations, consolidate skills in working with a circle and a table.

Developmental: continue work on the formation of students’ creative intellectual abilities through the use of various techniques for solving trigonometric equations.

Educational: develop skills of collective mental activity, mutual support and acceptance of a point of view different from one’s own.

During the classes

1. Situation of success.

Solve the equation: cosx=1; cosx=0; cosx= -1.

2. Situation, gap” between knowledge and ignorance.

Solve the equation: cosx=½; cosx=a.

Discussion.

3. Statement of the educational task.

How to solve an equation of this type?

1) What is the abscissa of a point on the unit circle obtained by rotating the point (1;0) around the origin by an angle equal to: ?

2). What is equal to: ?

Answer:

3).What is equal to: .

Answer:

;

;

(1) .

Teacher's words: mathematicians called the words reverse cos “the word arccosine (arccos). The arc cosine of a number is a number whose cosine is equal to a:
arccosa=α,if cosα=a and 0≤α≤π.

4). Write equality (1) using the arccos symbol.

5). Solve the equations: cosx=½, cosx=α.

Answer: x=arccos½, x=arccosa.

6). Name the angles of rotation of the point (1;0) of the unit circle having an abscissa equal to ½.

Answer: the abscissa is equal to ½ when the point is rotated by an angle equal to π/3 and -π/3.

i.e. cosx=½ at x=±arccos½
cosx=a at x=±arccosa.

7). What are the abscissas of the points obtained by rotating the point (1;0) by angles: π/3+2π; π/3+6π; -π/3+4π; -π/3+8π; π/3+2πn; -π/3+2πn.

Answer: the abscissa is ½, and cosx=½ at x=±arccos½+2πn,.
cosx=a at x=±arccosa+2πn,.

8). Conclusion: equation cosx=a

1) has roots if ≤1,
2) has no roots if >1.

9). Lesson summary:

a) For what values of a and α does the equality arccosa = α make sense?
b) What is called the arc cosine of a?
c) At what values of a does the equation cosx=a have roots?
d) Formula for finding the roots of the equation cosx=a.

The simplest trigonometric equations are the equations

Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) =a

Equation cos(x) = a

Explanation and rationale

The roots of the equation cosx = a. When | a | > 1 the equation has no roots, since | cosx |< 1 для любого x (прямая y = а при а >1 or at a< -1 не пересекает график функцииy = cosx).

Let | a |< 1. Тогда прямая у = а пересекает график функции

y = cos x. On the interval, the function y = cos x decreases from 1 to -1. But a decreasing function takes each of its values only at one point of its domain of definition, therefore the equation cos x = a has only one root on this interval, which, by definition of arccosine, is equal to: x 1 = arccos a (and for this root cos x = A).

Cosine is an even function, so on the interval [-n; 0] the equation cos x = and also has only one root - the number opposite x 1, that is

x 2 = -arccos a.

Thus, on the interval [-n; p] (length 2p) equation cos x = a with | a |< 1 имеет только корни x = ±arccos а.

The function y = cos x is periodic with a period of 2n, therefore all other roots differ from those found by 2n (n € Z). We obtain the following formula for the roots of the equation cos x = a when

x = ±arccos a + 2pp, n £ Z.

Special cases of solving the equation cosx = a.

It is useful to remember special notations for the roots of the equation cos x = a when

a = 0, a = -1, a = 1, which can be easily obtained using the unit circle as a reference.

Since the cosine is equal to the abscissa of the corresponding point of the unit circle, we obtain that cos x = 0 if and only if the corresponding point of the unit circle is point A or point B.

Similarly, cos x = 1 if and only if the corresponding point of the unit circle is point C, therefore,

x = 2πп, k € Z.

Also cos x = -1 if and only if the corresponding point of the unit circle is point D, thus x = n + 2n,

Equation sin(x) = a

Explanation and rationale

The roots of the equation sinx = a. When | a | > 1 the equation has no roots, since | sinx |< 1 для любого x (прямая y = а на рисунке при а >1 or at a< -1 не пересекает график функции y = sinx).

Examples:

\(2\sin(⁡x) = \sqrt(3)\)
tg\((3x)=-\) \(\frac(1)(\sqrt(3))\)
\(4\cos^2⁡x+4\sin⁡x-1=0\)
\(\cos⁡4x+3\cos⁡2x=1\)

How to solve trigonometric equations:

Any trigonometric equation should be reduced to one of the following types:

\(\sin⁡t=a\), \(\cos⁡t=a\), tg\(t=a\), ctg\(t=a\)

where \(t\) is an expression with an x, \(a\) is a number. Such trigonometric equations are called the simplest. They can be easily solved using () or special formulas:

See infographics on solving simple trigonometric equations here:, and.

Example . Solve the trigonometric equation \(\sin⁡x=-\)\(\frac(1)(2)\).
Solution:

Answer: \(\left[ \begin(gathered)x=-\frac(π)(6)+2πk, \\ x=-\frac(5π)(6)+2πn, \end(gathered)\right.\) \(k,n∈Z\)

What each symbol means in the formula for the roots of trigonometric equations, see.

Attention! The equations \(\sin⁡x=a\) and \(\cos⁡x=a\) have no solutions if \(a ϵ (-∞;-1)∪(1;∞)\). Because sine and cosine for any x are greater than or equal to \(-1\) and less than or equal to \(1\):

\(-1≤\sin x≤1\) \(-1≤\cos⁡x≤1\)

Example . Solve the equation \(\cos⁡x=-1,1\).
Solution: \(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
Answer : no solutions.

Example . Solve the trigonometric equation tg\(⁡x=1\).
Solution:

Let's solve the equation using the number circle. For this:
1) Construct a circle)
2) Construct the axes \(x\) and \(y\) and the tangent axis (it passes through the point \((0;1)\) parallel to the axis \(y\)).
3) On the tangent axis, mark the point \(1\).
4) Connect this point and the origin of coordinates - a straight line.
5) Mark the intersection points of this line and the number circle.
6) Let's sign the values of these points: \(\frac(π)(4)\) ,\(\frac(5π)(4)\)
7) Write down all the values of these points. Since they are located at a distance of exactly \(π\) from each other, all values can be written in one formula:

Answer: \(x=\)\(\frac(π)(4)\) \(+πk\), \(k∈Z\).

Example . Solve the trigonometric equation \(\cos⁡(3x+\frac(π)(4))=0\).
Solution:

Let's use the number circle again.
1) Construct a circle, axes \(x\) and \(y\).
2) On the cosine axis (\(x\) axis), mark \(0\).
3) Draw a perpendicular to the cosine axis through this point.
4) Mark the intersection points of the perpendicular and the circle.
5) Let's sign the values of these points: \(-\) \(\frac(π)(2)\),\(\frac(π)(2)\).
6) We write down the entire value of these points and equate them to the cosine (to what is inside the cosine).

\(3x+\)\(\frac(π)(4)\) \(=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\)

\(3x+\)\(\frac(π)(4)\) \(=\)\(\frac(π)(2)\) \(+2πk\) \(3x+\)\(\frac( π)(4)\) \(=-\)\(\frac(π)(2)\) \(+2πk\)

8) As usual, we will express \(x\) in equations.
Don't forget to treat numbers with \(π\), as well as \(1\), \(2\), \(\frac(1)(4)\), etc. These are the same numbers as all the others. No numerical discrimination!

\(3x=-\)\(\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=-\)\ (\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\)
\(3x=\)\(\frac(π)(4)\) \(+2πk\) \(|:3\) \(3x=-\)\(\frac(3π)(4)\) \(+2πk\) \(|:3\)
\(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\)

Answer: \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\) , \(k∈Z\).

Reducing trigonometric equations to the simplest is a creative task; here you need to use both and special methods for solving equations:
- Method (the most popular in the Unified State Examination).
- Method.
- Method of auxiliary arguments.

Let's consider an example of solving the quadratic trigonometric equation

Example . Solve the trigonometric equation \(2\cos^2⁡x-5\cos⁡x+2=0\)
Solution:

\(2\cos^2⁡x-5\cos⁡x+2=0\)	Let's make the replacement \(t=\cos⁡x\).

	Our equation has become typical. You can solve it using .
\(D=25-4 \cdot 2 \cdot 2=25-16=9\)
\(t_1=\)\(\frac(5-3)(4)\) \(=\)\(\frac(1)(2)\) ; \(t_2=\)\(\frac(5+3)(4)\) \(=2\)	We make a reverse replacement.
\(\cos⁡x=\)\(\frac(1)(2)\); \(\cos⁡x=2\)	We solve the first equation using the number circle. The second equation has no solutions because \(\cos⁡x∈[-1;1]\) and cannot be equal to two for any x.
	Let's write down all the numbers lying on at these points.

Answer: \(x=±\)\(\frac(π)(3)\) \(+2πk\), \(k∈Z\).

An example of solving a trigonometric equation with the study of ODZ:

Example (USE) . Solve the trigonometric equation \(=0\)

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	There is a fraction and there is a cotangent - that means we need to write it down. Let me remind you that a cotangent is actually a fraction: ctg\(x=\)\(\frac(\cos⁡x)(\sin⁡x)\) Therefore, the ODZ for ctg\(x\): \(\sin⁡x≠0\).
ODZ: ctg\(x ≠0\); \(\sin⁡x≠0\) \(x≠±\)\(\frac(π)(2)\) \(+2πk\); \(x≠πn\); \(k,n∈Z\)	Let us mark the “non-solutions” on the number circle.

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Let's get rid of the denominator in the equation by multiplying it by ctg\(x\). We can do this, since we wrote above that ctg\(x ≠0\).
\(2\cos^2⁡x-\sin⁡(2x)=0\)	Let's apply the double angle formula for sine: \(\sin⁡(2x)=2\sin⁡x\cos⁡x\).
\(2\cos^2⁡x-2\sin⁡x\cos⁡x=0\)	If your hands reach out to divide by the cosine, pull them back! You can divide by an expression with a variable if it is definitely not equal to zero (for example, these: \(x^2+1.5^x\)). Instead, let's take \(\cos⁡x\) out of brackets.
\(\cos⁡x (2\cos⁡x-2\sin⁡x)=0\)	Let’s “split” the equation into two.
\(\cos⁡x=0\); \(2\cos⁡x-2\sin⁡x=0\)	Let's solve the first equation using the number circle. Let's divide the second equation by \(2\) and move \(\sin⁡x\) to the right side.

\(x=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\). \(\cos⁡x=\sin⁡x\)	The resulting roots are not included in the ODZ. Therefore, we will not write them down in response. The second equation is typical. Let's divide it by \(\sin⁡x\) (\(\sin⁡x=0\) cannot be a solution to the equation because in this case \(\cos⁡x=1\) or \(\cos⁡ x=-1\)).
	We use a circle again.
\(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\)	These roots are not excluded by ODZ, so you can write them in the answer.

Answer: \(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\).

cos equation X = A

Each root of the equation

cos X = A (1)

can be considered as the abscissa of some intersection point of the sinusoid y = cosX with a straight line y =A , and, conversely, the abscissa of each such intersection point is one of the roots of equation (1). Thus, the set of all roots of equation (1) coincides with the set of abscissas of all intersection points of the cosine wave y = cosX with a straight line y = A .

If | A| >1 , then the cosine y = cosX does not intersect with a line y = A .

In this case, equation (1) has no roots.

At |A| < 1 there are infinitely many points of intersection.

for a > 0

for a< 0.

We will divide all these intersection points into two groups:

A -2 , A - 1 , A 1 , A 2 , ... ,

B -2 , B - 1 , B 1 , B 2 , ... ,

Dot A has an abscissa arccos A , and all other points of the first group are separated from it at distances that are multiples of 2 π

arccos a+ 2k π . (2)

Dot IN, as can be easily understood from the figures, has an abscissa - arccosA , and all other points of the second group are removed from it at distances that are multiples of 2 π . Therefore their abscissas are expressed as

arccos A+ 2nπ . (3)

Thus, equation (1) has two groups of roots defined by formulas (2) and (3). But these two formulas can obviously be written as one formula

X = ± arccos a+ 2m π , (4)

Where m runs through all integers (m = 0, ±1, ±2, ±3, ...).

The reasoning that we carried out in deriving this formula is correct only if
| a| =/= 1. However, formally the relation (4) determines all the roots of the equation cosx=a and at | A| =1. (Prove it!) Therefore we can say that the formula (4) gives all roots of equation (1) for any values A , If only |A| < 1 .

But still in three special cases ( A = 0, A = -1, A= +1) we recommend not to use the formula (4) , but use other relations. It is useful to remember that the roots of the equation cos X = 0 are given by the formula

X = π / 2 +n π ; (5)

roots of the equation cos X = -1 are given by the formula

X = π + 2m π ; (6)

and finally, the roots of the equation cos X = 1 are given by the formula

X = 2m π ; (7)

In conclusion, we note that the formulas (4) , (5), (6) and (7) are correct only under the assumption that the desired angle X expressed in radians. If it is expressed in degrees, then these formulas need to be naturally changed. So, the formula (4) should be replaced by the formula

X = ± arccos a+ 360° n,

formula (5) formula

X = 90° + 180° n etc.