કોસ સમીકરણો કેવી રીતે ઉકેલવા. સમીકરણ cos x = a

ઝખારોવા લ્યુડમિલા વ્લાદિમીરોવના
બાર્નૌલની MBOU "માધ્યમિક શાળા નં. 59".
ગણિત શિક્ષક [ઇમેઇલ સુરક્ષિત]

№1 સૌથી સરળ ત્રિકોણમિતિ સમીકરણો

લક્ષ્ય: 1. ફોર્મના સૌથી સરળ ત્રિકોણમિતિ સમીકરણોના ઉકેલો માટે સૂત્રો મેળવો sinx =a, cosx=a, tgx=a, ctgx=a;

2. સૂત્રોનો ઉપયોગ કરીને સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલતા શીખો.

સાધન: 1) ત્રિકોણમિતિ વિધેયોના ગ્રાફ સાથે કોષ્ટકો y= sinx, y=cosx, y=tgx, y=ctgx; 2) વ્યસ્ત ત્રિકોણમિતિ કાર્યોના મૂલ્યોનું કોષ્ટક; 3) સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવા માટેના સૂત્રોનું સારાંશ કોષ્ટક.

લેક્ચર લેસન પ્લાન:

1 .સમીકરણના મૂળ માટે સૂત્રોની વ્યુત્પત્તિ

a) sinx =a,

b) cosx= a,

c) tgx= a,

d) ctgx= એ.

2 . પ્રાપ્ત સૂત્રોને એકીકૃત કરવા માટે મૌખિક આગળનું કાર્ય.

3 . અભ્યાસ કરેલ સામગ્રીને એકીકૃત કરવા માટે લેખિત કાર્ય

વર્ગો દરમિયાન.

બીજગણિત, ભૂમિતિ, ભૌતિકશાસ્ત્ર અને અન્ય વિષયોમાં, આપણે વિવિધ સમસ્યાઓનો સામનો કરીએ છીએ, જેના ઉકેલમાં સમીકરણો ઉકેલવાનો સમાવેશ થાય છે. અમે ત્રિકોણમિતિ વિધેયોના ગુણધર્મોનો અભ્યાસ કર્યો છે, તેથી તે સમીકરણો તરફ વળવું સ્વાભાવિક છે જેમાં ફંક્શન ચિહ્ન હેઠળ અજ્ઞાત સમાયેલ છે.

વ્યાખ્યા: ફોર્મના સમીકરણો sinx = a , cosx= a , tgx= a , ctgx= એ સૌથી સરળ ત્રિકોણમિતિ સમીકરણો કહેવાય છે.

સૌથી સરળ ત્રિકોણમિતિ સમીકરણો કેવી રીતે ઉકેલવા તે શીખવું ખૂબ જ મહત્વપૂર્ણ છે, કારણ કે કોઈપણ ત્રિકોણમિતિ સમીકરણોને ઉકેલવા માટેની તમામ પદ્ધતિઓ અને તકનીકો તેમને સરળમાં ઘટાડવામાં સમાવિષ્ટ છે.

ચાલો ત્રિકોણમિતિ સમીકરણો ઉકેલતી વખતે "સક્રિયપણે" કામ કરતા સૂત્રોમાંથી શરૂઆત કરીએ.

1. sinx સ્વરૂપના સમીકરણો = a.

ચાલો sinx = સમીકરણ હલ કરીએ aગ્રાફિકલી. આ કરવા માટે, એક કોઓર્ડિનેટ સિસ્ટમમાં આપણે y=sinx અને y= ફંક્શનનો આલેખ બનાવીશું. એ.

1) જો એ> 1 અને એપાપ x= એકોઈ ઉકેલ નથી, કારણ કે સીધી રેખા અને સાઈન વેવમાં સામાન્ય બિંદુઓ નથી.

2) જો -1a a સાઈન વેવને અનંત રીતે ઘણી વખત ક્રોસ કરે છે. આનો અર્થ એ છે કે સમીકરણ sinx= aઅસંખ્ય ઉકેલો છે.

સાઈનનો સમયગાળો 2 હોવાથી , પછી સમીકરણ ઉકેલવા માટે sinx= aલંબાઈ 2 ના કોઈપણ સેગમેન્ટ પર તમામ ઉકેલો શોધવા માટે તે પૂરતું છે.

[-/2 પર સમીકરણ ઉકેલવું; /2] આર્ક્સીન x= ની વ્યાખ્યા દ્વારાઆર્ક્સીન a, અને x=-arcsin પર a. ફંક્શન у=sinx ની સામયિકતાને ધ્યાનમાં લેતા, અમે નીચેના સમીકરણો મેળવીએ છીએ

x = -આર્કસીન a+2n, n Z.

ઉકેલોની બંને શ્રેણીને જોડી શકાય છે

X = (-1) n આર્ક્સીન a+n, nZ.

નીચેના ત્રણ કિસ્સાઓમાં, તેઓ સામાન્ય સૂત્રને બદલે સરળ સંબંધોનો ઉપયોગ કરવાનું પસંદ કરે છે:

જો એ=-1, પછી sin x =-1, x=-/2+2n

જો એ=1, પછી sin x =1, x =/2+2n

જો a= 0, પછી sin x =0. x = n,

ઉદાહરણ: સમીકરણ ઉકેલો sinx = 1/2.

ચાલો ઉકેલો માટે સૂત્રો બનાવીએ x=arcsin 1/2+ 2n

X= - arcsin a+2n

ચાલો મૂલ્યની ગણતરી કરીએ arcsin1/2. ચાલો સોલ્યુશન ફોર્મ્યુલામાં મળેલ મૂલ્યને બદલીએ

x=5/6+2 એન

અથવા સામાન્ય સૂત્ર અનુસાર

X= (-1) n આર્ક્સીન 1/2+n,

X= (-1) n /6+n,

2. ફોર્મના સમીકરણો cosx= a.

ચાલો cosx= સમીકરણ હલ કરીએ aગ્રાફિકલી પણ, વિધેયો y= cosx અને y= ની રચના કરીને એ.

1) જો a 1, તો સમીકરણ cosx= aકોઈ ઉકેલ નથી, કારણ કે ગ્રાફમાં સામાન્ય બિંદુઓ નથી.

2) જો -1 a cosx= aઅસંખ્ય ઉકેલો છે.

અમે તમામ ઉકેલો શોધીશું cosx= aલંબાઈ 2 ના અંતરાલ પર કારણ કે કોસાઈનનો સમયગાળો 2 છે.

આર્ક કોસાઇનની વ્યાખ્યા મુજબ, સમીકરણનો ઉકેલ x= હશેઆર્કોસ એ. કોસાઇન ફંક્શનની સમાનતાને ધ્યાનમાં લેતા, [-;0] પરના સમીકરણનો ઉકેલ x=-arcos હશે a.

આમ, સમીકરણ ઉકેલવું cosx= a x= + આર્કોસ a+ 2 એન,

ત્રણ કિસ્સાઓમાં, અમે સામાન્ય સૂત્રનો ઉપયોગ કરીશું નહીં, પરંતુ સરળ સંબંધોનો ઉપયોગ કરીશું:

જો એ=-1, પછી cosx =-1, x =-/2+2n

જો એ=1, પછી cosx =1, x = 2n,

જો a=0, તો cosx=0. x =/2+n

ઉદાહરણ: સમીકરણ ઉકેલો cos x =1/2,

ચાલો ઉકેલો માટે સૂત્રો બનાવીએ x=arccos 1/2+ 2n

ચાલો મૂલ્યની ગણતરી કરીએ arccos1/2.

ચાલો સોલ્યુશન ફોર્મ્યુલામાં મળેલ મૂલ્યને બદલીએ

X= + /3+ 2n, nZ.

ફોર્મના સમીકરણો tgx= a.

સ્પર્શકનો સમયગાળો સમાન હોવાથી, સમીકરણના તમામ ઉકેલો શોધવા માટે tgx= a, લંબાઈના કોઈપણ અંતરાલ પર તમામ ઉકેલો શોધવા માટે તે પૂરતું છે. આર્કટેન્જેન્ટની વ્યાખ્યા પ્રમાણે, (-/2; /2) પરના સમીકરણનો ઉકેલ આર્ક્ટન છે a. કાર્યના સમયગાળાને ધ્યાનમાં લેતા, સમીકરણના તમામ ઉકેલો ફોર્મમાં લખી શકાય છે

x= આર્ક્ટાન a+ n, nZ.

ઉદાહરણ:સમીકરણ ઉકેલો tan x = 3/3

ચાલો x= ઉકેલવા માટે એક સૂત્ર બનાવીએઆર્કટન 3/3 +n, nZ.

ચાલો આર્કટેન્જેન્ટ મૂલ્યની ગણતરી કરીએઆર્કટન 3/3= /6, પછી

X=/6+ n, nZ.

સમીકરણ ઉકેલવા માટેના સૂત્રની વ્યુત્પત્તિ સાથે tgx= aવિદ્યાર્થીઓને આપી શકાય છે.

ઉદાહરણ.

સમીકરણ ઉકેલો ctg x = 1.

x = arcсtg 1 + n, nZ,

X = /4 + n, nZ.

અભ્યાસ કરેલ સામગ્રીના પરિણામે, વિદ્યાર્થીઓ કોષ્ટક ભરી શકે છે:

"ત્રિકોણમિતિ સમીકરણો ઉકેલવા."

સમીકરણ

અભ્યાસ કરેલ સામગ્રીને એકીકૃત કરવા માટે કસરતો.

(મૌખિક) ફોર્મ્યુલાનો ઉપયોગ કરીને કયા લેખિત સમીકરણો ઉકેલી શકાય છે:

a) x= (-1) n આર્ક્સીન a+n, nZ;

b) x= + આર્કોસ એ+ 2n?

cos x = 2/2, tan x= 1, sin x = 1/3, cos x = 3/3, sin x = -1/2, cos x= 2/3, sin x = 3, cos x = 2 .

નીચેનામાંથી કયા સમીકરણોનો કોઈ ઉકેલ નથી?

સમીકરણો ઉકેલો:

a) પાપ x = 0; e) પાપ x = 2/2; h) પાપ x = 2;

b) cos x = 2/2; e) cos x = -1/2; i) cos x = 1;

ડી) ટેન x = 3; g) પારણું x = -1; j) ટેન x = 1/ 3.

3. સમીકરણો ઉકેલો:

a) પાપ 3x = 0; e) 2cos x = 1;

b) cos x/2 =1/2; e) 3 tg 3x =1;

d) પાપ x/4 = 1; g) 2cos(2x+ /5) = 3.

આ સમીકરણો ઉકેલતી વખતે, ફોર્મના સમીકરણો ઉકેલવાના નિયમો લખવા ઉપયોગી છેપાપ વી x = a, અને સાથેપાપ વી x = a, | a|1.

પાપ વી x = a, |a|1.

વી x = (-1) n આર્ક્સીન a+n, nZ,

x= (-1) n 1/ વીઆર્ક્સીન a+n/ વી, nZ.

પાઠનો સારાંશ:

આજે વર્ગમાં આપણે સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવા માટેના સૂત્રો મેળવ્યા છે.

અમે સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવાના ઉદાહરણો જોયા.

અમે સમીકરણો ઉકેલવા માટે ઉપયોગ કરીશું તે કોષ્ટક ભર્યું.

ગૃહ કાર્ય.

№2 ત્રિકોણમિતિ સમીકરણો ઉકેલવા

લક્ષ્ય: ત્રિકોણમિતિ સમીકરણો ઉકેલવા માટેની અભ્યાસ પદ્ધતિઓ: 1) ચતુર્ભુજથી ઘટાડી શકાય તેવું; 2) સજાતીય ત્રિકોણમિતિ સમીકરણો માટે ઘટાડી શકાય તેવું.

ત્રિકોણમિતિ સમીકરણો ઉકેલવાની વિવિધ પદ્ધતિઓનો ઉપયોગ કરતી વખતે વિદ્યાર્થીઓની અવલોકન શક્તિ વિકસાવવી.

વિદ્યાર્થીઓ સાથે આગળનું કામ.

ત્રિકોણમિતિ સમીકરણોના મૂળ માટેના સૂત્રો શું છે? cos x= a, sin x= a, tgx = a, ctg x = a.

સમીકરણો ઉકેલો (મૌખિક રીતે):

cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1.5, sin x=0.

ભૂલો શોધો અને ભૂલોના કારણો વિશે વિચારો.

cos x=1/2, x= + /6+2k, k ઝેડ.

sin x= 3/2, x= /3+k, kZ.

tgx = /4, x=1+ k, kZ.

2. નવી સામગ્રીનો અભ્યાસ.

આ પાઠ ત્રિકોણમિતિ સમીકરણોને ઉકેલવા માટેની કેટલીક સૌથી સામાન્ય પદ્ધતિઓને આવરી લેશે.

ત્રિકોણમિતિ સમીકરણો ઘટાડીને ચતુર્ભુજ.

આ વર્ગમાં સમીકરણો શામેલ હોઈ શકે છે જેમાં એક ફંક્શન (સાઇન અથવા કોસાઇન) અથવા સમાન દલીલના બે ફંક્શનનો સમાવેશ થાય છે, પરંતુ તેમાંથી એક મૂળભૂત ત્રિકોણમિતિ ઓળખનો ઉપયોગ કરીને બીજામાં ઘટાડી શકાય છે.

ઉદાહરણ તરીકે, જો cosх સમીકરણમાં સમ શક્તિઓ દાખલ કરે છે, તો આપણે તેને 1-sin 2 x સાથે બદલીએ છીએ, જો sin 2 x, તો આપણે તેને 1-cos 2 x સાથે બદલીએ છીએ.

ઉદાહરણ.

સમીકરણ ઉકેલો: 8 sin 2 x - 6sin x -5 =0.

ઉકેલ: ચાલો સૂચિત કરીએ sin x=t, પછી 8t 2 - 6t – 5=0,

ડી = 196,

ટી 1 = -1/2, ટી 2 = -5/4.

ચાલો વિપરીત અવેજીકરણ કરીએ અને નીચેના સમીકરણોને હલ કરીએ.

X=(-1) k+1 /6+ k, kZ.

-5/4>1 થી, સમીકરણનું કોઈ મૂળ નથી.

જવાબ: x=(-1) k+1 /6+ k, kZ.

એકત્રીકરણ કસરતો ઉકેલવી.

સમીકરણ ઉકેલો:

1) 2sin 2 x+ 3cos x = 0;

2) 5sin 2 x+ 6cos x -6 = 0;

3) 2sin 2 x+ 3cos 2 x = -2sin x;

4) 3 tg 2 x +2 tgx-1=0.

સજાતીય ત્રિકોણમિતિ સમીકરણો.

વ્યાખ્યા: 1) ફોર્મનું સમીકરણa sinx + b cosx=0, (a=0, b=0) sin x અને cos x ના સંદર્ભમાં પ્રથમ ડિગ્રીનું સજાતીય સમીકરણ કહેવાય છે.

આ સમીકરણ બંને બાજુઓ દ્વારા વિભાજીત કરીને ઉકેલવામાં આવે છે cosx 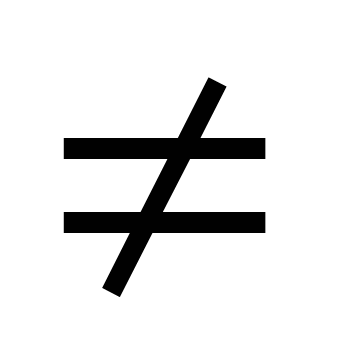0. પરિણામ એ સમીકરણ છે atgx+ b=0.

2) ફોર્મનું સમીકરણa પાપ 2 x + b sinx cosx + c cos 2 x =0 બીજા અંશનું સજાતીય સમીકરણ કહેવાય છે, જ્યાં a, b, c કોઈપણ સંખ્યાઓ છે.

જો a = 0 હોય, તો આપણે બંને બાજુઓને વડે ભાગીને સમીકરણ ઉકેલીએ છીએ cos 2 x 0. પરિણામે, આપણે સમીકરણ મેળવીએ છીએ atg 2 x+ btgx+с =0.

ટિપ્પણી:ફોર્મનું સમીકરણa પાપ mx + b cos mx=0 અથવા

a પાપ 2 mx + b પાપ mx cos mx + c cos 2 mx =0 એકરૂપ પણ છે. તેમને ઉકેલવા માટે, સમીકરણની બંને બાજુઓને cos દ્વારા વિભાજિત કરવામાં આવે છે mx=0 અથવા cos 2 mx=0

3) વિવિધ સમીકરણો કે જે મૂળ રૂપે સજાતીય સમીકરણો નથી તેને સજાતીય સમીકરણોમાં ઘટાડી શકાય છે. દાખ્લા તરીકે,પાપ 2 mx + b પાપ mx cos mx + c cos 2 mx = ડી, અને a sinx + b cosx= ડી. આ સમીકરણોને ઉકેલવા માટે, તમારે જમણી બાજુનો ગુણાકાર કરવાની જરૂર છે "ત્રિકોણમિતિ એકમ"તે પર પાપ 2 x + cos 2 xઅને ગાણિતિક પરિવર્તનો કરો.

શીખેલી સામગ્રીને એકીકૃત કરવા માટેની કસરતો:

1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;

2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;

3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;

4) sin 2 x -3 sinx cosx +2 cos 2 x =0

3. પાઠનો સારાંશ. ગૃહ કાર્ય.

આ પાઠમાં, જૂથની સજ્જતાના આધારે, તમે ફોર્મના સમીકરણો ઉકેલવા પર વિચાર કરી શકો છો a sin mx +b cos mx=c, જ્યાં a, b, c એક જ સમયે શૂન્યની બરાબર નથી.

મજબૂત કરવાની કસરતો:

1. 3sin x + cos x=2;

2. 3sin 2x + cos 2x= 2;

3. sin x/3 + cos x/3=1;

4. 12 sin x +5 cos x+13=0.

№ 3 ત્રિકોણમિતિ સમીકરણો ઉકેલવા

લક્ષ્ય: 1) પરિબળીકરણ દ્વારા ત્રિકોણમિતિ સમીકરણો ઉકેલવાની પદ્ધતિનો અભ્યાસ કરો; વિવિધ ત્રિકોણમિતિ સૂત્રોનો ઉપયોગ કરીને ત્રિકોણમિતિ સમીકરણો ઉકેલવાનું શીખો;

2) તપાસો: સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવા માટે વિદ્યાર્થીઓનું સૂત્રોનું જ્ઞાન; સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવાની ક્ષમતા.

પાઠ ની યોજના:

હોમવર્ક તપાસી રહ્યું છે.

ગાણિતિક શ્રુતલેખન.

નવી સામગ્રી શીખવી.

સ્વતંત્ર કાર્ય.

પાઠનો સારાંશ. ગૃહ કાર્ય.

પાઠની પ્રગતિ:

હોમવર્ક તપાસી રહ્યું છે (ત્રિકોણમિતિ સમીકરણોના ઉકેલો ટૂંકમાં બોર્ડ પર લખેલા છે).

ગાણિતિક શ્રુતલેખન.

1 માં

1. કયા સમીકરણોને સૌથી સરળ ત્રિકોણમિતિ સમીકરણો કહેવામાં આવે છે?

2. ફોર્મના સમીકરણનું નામ શું છેa sinx + b cosx=0? તેને હલ કરવાની રીત જણાવો.

3.સમીકરણના મૂળ માટે સૂત્ર લખો tgx = a(ctg x= a).

4. ફોર્મના સમીકરણોના મૂળ માટેના સૂત્રો લખો cosx= a, જ્યાં એ=1, એ=0, એ=-1.

5. સમીકરણના મૂળ માટે સામાન્ય સૂત્ર લખોપાપ x= a, | a|

6. ફોર્મના સમીકરણો કેવી રીતે ઉકેલાય છેa cosx= b, | b|

એટી 2

1. સમીકરણોના મૂળ માટેના સૂત્રો લખો cosx= a,| a|

2. સમીકરણના મૂળ માટે સામાન્ય સૂત્ર લખો

= a, | a|

3. ફોર્મના સમીકરણો શું કહેવાય છે?પાપ x= a, tgx = a, પાપ x= a?

4. સમીકરણના મૂળ માટેના સૂત્રો લખોપાપ x= a, જો એ=1, એ=0, એ=-1.

5. ફોર્મના સમીકરણો કેવી રીતે ઉકેલાય છેપાપ a x= b, | b|

6. કયા સમીકરણોને બીજી ડિગ્રીના સજાતીય સમીકરણો કહેવામાં આવે છે? તેઓ કેવી રીતે ઉકેલાય છે?

નવી સામગ્રી શીખવી.

ફેક્ટરાઇઝેશન પદ્ધતિ.

ત્રિકોણમિતિ સમીકરણો ઉકેલવા માટે સૌથી વધુ ઉપયોગમાં લેવાતી પદ્ધતિઓમાંની એક ફેક્ટરાઇઝેશન પદ્ધતિ છે.

જો સમીકરણ f(x) =0 ને f 1 (x) f 2 (x) =0 તરીકે રજૂ કરી શકાય, તો સમસ્યા f 1 (x) = 0, f 2 (x) = 0 બે સમીકરણો ઉકેલવામાં ઘટે છે. .

(વિદ્યાર્થીઓ માટે નિયમ યાદ રાખવું ઉપયોગી છે “ અવયવોનું ઉત્પાદન શૂન્ય બરાબર છે જો ઓછામાં ઓછું એક પરિબળ શૂન્ય સમાન હોય અને અન્યનો અર્થ થાય»)

વિવિધ જટિલતાના સમીકરણોને ઉકેલવા દ્વારા અભ્યાસ કરેલ સામગ્રીનું એકીકરણ.

(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(સ્વ)

3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;

5) sin 2x - cosx=0; 6) 4 cos 2 x -1 =0; (2 રીતે)

7) cosx+ cos3x=0; 8) sin 3x = sin 17x;

9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x

11) sin x cos5x = sin 9x cos3x sin 2x sin 2x

12) 3 cosx sin x+ cos 2 x=0(સ્વ)

13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.

સ્વતંત્ર કાર્ય.

વિકલ્પ-1 વિકલ્પ-2

1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;

2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;

3) 5 sin 2 x+ sin x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5;

4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;

5) sin x+cosx=1. 5) sin x+cosx=2.

8. પાઠનો સારાંશ. ગૃહ કાર્ય.

પાઠનો પ્રકાર:શીખવાનું કાર્ય સેટ કરવું.

પાઠ હેતુઓ:

શૈક્ષણિક: સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવા માટેની પદ્ધતિઓના વિદ્યાર્થીઓના જ્ઞાનને વ્યવસ્થિત બનાવો, વર્તુળો અને કોષ્ટકો સાથે કામ કરવાની કુશળતાને એકીકૃત કરો.

વિકાસલક્ષી: ત્રિકોણમિતિ સમીકરણો ઉકેલવા માટે વિવિધ તકનીકોના ઉપયોગ દ્વારા વિદ્યાર્થીઓની સર્જનાત્મક બૌદ્ધિક ક્ષમતાઓના નિર્માણ પર કાર્ય ચાલુ રાખો.

શૈક્ષણિક: સામૂહિક માનસિક પ્રવૃત્તિ, પરસ્પર સમર્થન અને પોતાનાથી અલગ દૃષ્ટિકોણની સ્વીકૃતિની કુશળતા વિકસાવો.

વર્ગો દરમિયાન

1. સફળતાની સ્થિતિ.

સમીકરણ ઉકેલો: cosx=1; cosx=0; cosx= -1.

2. પરિસ્થિતિ, જ્ઞાન અને અજ્ઞાન વચ્ચેનું અંતર.

સમીકરણ ઉકેલો: cosx=½; cosx=a.

ચર્ચા.

3. શૈક્ષણિક કાર્યનું નિવેદન.

આ પ્રકારના સમીકરણને કેવી રીતે હલ કરવું?

1) એકમ વર્તુળ પરના બિંદુ (1;0) ને મૂળની આસપાસ ફેરવવાથી મેળવેલા બિંદુનો એબ્સિસા શું છે: ?

2). શું સમાન છે: ?

જવાબ:

3). શું બરાબર છે: .

જવાબ:

;

;

(1) .

શિક્ષકના શબ્દો: ગણિતશાસ્ત્રીઓએ શબ્દોને રિવર્સ કોસ “ શબ્દ આર્કોસીન (આર્કોસ) કહે છે. સંખ્યાની ચાપ કોસાઈન એ એવી સંખ્યા છે જેની કોસાઈન a ની બરાબર છે:
arccosa=α,જો cosα=a અને 0≤α≤π.

4). આર્કોસ પ્રતીકનો ઉપયોગ કરીને સમાનતા (1) લખો.

5). સમીકરણો ઉકેલો: cosx=½, cosx=α.

જવાબ: x=arccos½, x=arccosa.

6). એકમ વર્તુળના બિંદુ (1;0) ના પરિભ્રમણના ખૂણાઓને નામ આપો જેમાં ½ ની બરાબર એબ્સિસા હોય.

જવાબ: જ્યારે બિંદુને π/3 અને -π/3 સમાન ખૂણાથી ફેરવવામાં આવે ત્યારે એબ્સીસા ½ ની બરાબર હોય છે.

એટલે કે cosx=½ at x=±arccos½
cosx=a at x=±arccosa.

7). બિંદુ (1;0) ને ખૂણાઓ દ્વારા ફેરવવાથી મેળવેલા પોઈન્ટના એબ્સીસાસ શું છે: π/3+2π; π/3+6π; -π/3+4π; -π/3+8π; π/3+2πn; -π/3+2πn.

જવાબ: એબ્સીસા ½ છે, અને cosx=½ પર x=±arccos½+2πn,.
cosx=a at x=±arccosa+2πn,.

8). નિષ્કર્ષ: સમીકરણ cosx=a

1) મૂળ ધરાવે છે જો ≤1,
2) કોઈ મૂળ નથી જો >1.

9). પાઠ સારાંશ:

a) a અને α ના કયા મૂલ્યો માટે સમાનતા arccosa = α અર્થપૂર્ણ છે?
b) a ના ચાપ કોસાઈનને શું કહેવાય છે?
c) a ના કયા મૂલ્યો પર સમીકરણ cosx=a મૂળ ધરાવે છે?
d) cosx=a સમીકરણના મૂળ શોધવા માટેનું સૂત્ર.

સૌથી સરળ ત્રિકોણમિતિ સમીકરણો સમીકરણો છે

Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) =a

સમીકરણ cos(x) = a

સમજૂતી અને તર્ક

સમીકરણના મૂળ cosx = a. જ્યારે | a | > 1 સમીકરણનું કોઈ મૂળ નથી, ત્યારથી | cosx |< 1 для любого x (прямая y = а при а >1 અથવા એ< -1 не пересекает график функцииy = cosx).

ચાલો | a |< 1. Тогда прямая у = а пересекает график функции

y = cos x. અંતરાલ પર, કાર્ય y = cos x 1 થી -1 સુધી ઘટે છે. પરંતુ ઘટતું કાર્ય તેના દરેક મૂલ્યોને તેની વ્યાખ્યાના ડોમેનના એક બિંદુએ જ લે છે, તેથી સમીકરણ cos x = a આ અંતરાલ પર માત્ર એક જ મૂળ ધરાવે છે, જે આર્કોસીનની વ્યાખ્યા પ્રમાણે, બરાબર છે: x 1 = arccos a (અને આ રુટ cos x = A માટે).

કોસાઇન એક સમાન કાર્ય છે, તેથી અંતરાલ [-n; 0] સમીકરણ cos x = અને તેમાં માત્ર એક જ મૂળ છે - x 1 ની વિરુદ્ધની સંખ્યા, એટલે કે

x 2 = -arccos a.

આમ, અંતરાલ પર [-n; p] (લંબાઈ 2p) સમીકરણ cos x = a સાથે | a |< 1 имеет только корни x = ±arccos а.

ફંક્શન y = cos x 2n ના સમયગાળા સાથે સામયિક છે, તેથી અન્ય તમામ મૂળ 2n (n € Z) દ્વારા મળેલા મૂળથી અલગ છે. આપણે cos x = a when સમીકરણના મૂળ માટે નીચેનું સૂત્ર મેળવીએ છીએ

x = ±arccos a + 2pp, n £Z.

સમીકરણ ઉકેલવાના ખાસ કિસ્સાઓ cosx = a.

cos x = a when સમીકરણના મૂળ માટે વિશેષ સંકેતો યાદ રાખવા માટે તે ઉપયોગી છે

a = 0, a = -1, a = 1, જે સંદર્ભ તરીકે એકમ વર્તુળનો ઉપયોગ કરીને સરળતાથી મેળવી શકાય છે.

કોસાઇન એકમ વર્તુળના અનુરૂપ બિંદુના એબ્સીસા સમાન હોવાથી, અમે તે cos x = 0 જો અને માત્ર ત્યારે જ મેળવીએ છીએ જો એકમ વર્તુળનો અનુરૂપ બિંદુ બિંદુ A અથવા બિંદુ B હોય.

તેવી જ રીતે, cos x = 1 જો અને માત્ર જો એકમ વર્તુળનો અનુરૂપ બિંદુ બિંદુ C હોય, તેથી,

x = 2πп, k € Z.

તેમજ cos x = -1 જો અને માત્ર જો એકમ વર્તુળનો અનુરૂપ બિંદુ બિંદુ D હોય, આમ x = n + 2n,

સમીકરણ sin(x) = a

સમજૂતી અને તર્ક

સમીકરણના મૂળ sinx = a. જ્યારે | a | > 1 સમીકરણનું કોઈ મૂળ નથી, ત્યારથી | sinx |< 1 для любого x (прямая y = а на рисунке при а >1 અથવા એ< -1 не пересекает график функции y = sinx).

ઉદાહરણો:

\(2\sin(⁡x) = \sqrt(3)\)
tg\((3x)=-\) \(\frac(1)(\sqrt(3))\)
\(4\cos^2⁡x+4\sin⁡x-1=0\)
\(\cos⁡4x+3\cos⁡2x=1\)

ત્રિકોણમિતિ સમીકરણો કેવી રીતે ઉકેલવા:

કોઈપણ ત્રિકોણમિતિ સમીકરણ નીચેના પ્રકારોમાંથી એકમાં ઘટાડવું જોઈએ:

\(\sin⁡t=a\), \(\cos⁡t=a\), tg\(t=a\), ctg\(t=a\)

જ્યાં \(t\) એ x સાથેની અભિવ્યક્તિ છે, \(a\) એ સંખ્યા છે. આવા ત્રિકોણમિતિ સમીકરણો કહેવામાં આવે છે સૌથી સરળ. તેઓ () અથવા વિશિષ્ટ સૂત્રોનો ઉપયોગ કરીને સરળતાથી ઉકેલી શકાય છે:

અહીં સરળ ત્રિકોણમિતિ સમીકરણો ઉકેલવા પર ઇન્ફોગ્રાફિક્સ જુઓ:, અને.

ઉદાહરણ . ત્રિકોણમિતિ સમીકરણ ઉકેલો \(\sin⁡x=-\)\(\frac(1)(2)\).
ઉકેલ:

જવાબ: \(\લેફ્ટ[ \begin(એકત્ર કરેલ)x=-\frac(π)(6)+2πk, \\ x=-\frac(5π)(6)+2πn, \અંત(એકત્ર કરેલ)\જમણે.\) \(k,n∈Z\)

ત્રિકોણમિતિ સમીકરણોના મૂળના સૂત્રમાં દરેક પ્રતીકનો અર્થ શું થાય છે, જુઓ.

ધ્યાન આપો!સમીકરણો \(\sin⁡x=a\) અને \(\cos⁡x=a\) પાસે કોઈ ઉકેલ નથી જો \(a ϵ (-∞;-1)∪(1;∞)\). કારણ કે કોઈપણ x માટે સાઈન અને કોસાઈન \(-1\) કરતા વધારે અથવા સમાન હોય છે અને \(1\) કરતા ઓછા અથવા ઓછા હોય છે:

\(-1≤\sin x≤1\) \(-1≤\cos⁡x≤1\)

ઉદાહરણ . સમીકરણ ઉકેલો \(\cos⁡x=-1,1\).
ઉકેલ: \(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
જવાબ આપો : કોઈ ઉકેલ નથી.

ઉદાહરણ . ત્રિકોણમિતિ સમીકરણ tg\(⁡x=1\) ઉકેલો.
ઉકેલ:

ચાલો સંખ્યા વર્તુળનો ઉપયોગ કરીને સમીકરણ ઉકેલીએ. આ માટે:
1) એક વર્તુળ બનાવો)
2) અક્ષો \(x\) અને \(y\) અને સ્પર્શક અક્ષ (તે બિંદુ \(0;1)\) અક્ષની સમાંતર \(y\)માંથી પસાર થાય છે).
3) સ્પર્શક ધરી પર, બિંદુ \(1\) ને ચિહ્નિત કરો.
4) આ બિંદુ અને કોઓર્ડિનેટ્સના મૂળને જોડો - એક સીધી રેખા.
5) આ રેખા અને સંખ્યા વર્તુળના આંતરછેદ બિંદુઓને ચિહ્નિત કરો.
6) ચાલો આ બિંદુઓના મૂલ્યો પર સહી કરીએ: \(\frac(π)(4)\) ,\(\frac(5π)(4)\)
7) આ બિંદુઓના તમામ મૂલ્યો લખો. તેઓ એકબીજાથી બરાબર \(π\) ના અંતરે સ્થિત હોવાથી, બધા મૂલ્યો એક સૂત્રમાં લખી શકાય છે:

જવાબ: \(x=\)\(\frac(π)(4)\) \(+πk\), \(k∈Z\).

ઉદાહરણ . ત્રિકોણમિતિ સમીકરણ ઉકેલો \(\cos⁡(3x+\frac(π)(4))=0\).
ઉકેલ:

ચાલો નંબર વર્તુળનો ફરીથી ઉપયોગ કરીએ.
1) વર્તુળ, અક્ષ \(x\) અને \(y\) બનાવો.
2) કોસાઇન અક્ષ (\(x\) અક્ષ પર, ચિહ્નિત કરો \(0\).
3) આ બિંદુ દ્વારા કોસાઇન અક્ષ પર લંબ દોરો.
4) કાટખૂણે અને વર્તુળના આંતરછેદ બિંદુઓને ચિહ્નિત કરો.
5) ચાલો આ બિંદુઓના મૂલ્યો પર સહી કરીએ: \(-\) \(\frac(π)(2)\),\(\frac(π)(2)\).
6) અમે આ બિંદુઓની સંપૂર્ણ કિંમત લખીએ છીએ અને તેમને કોસાઇન (કોસાઇનની અંદર શું છે) સાથે સરખાવીએ છીએ.

\(3x+\)\(\frac(π)(4)\) \(=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\)

\(3x+\)\(\frac(π)(4)\) \(=\)\(\frac(π)(2)\) \(+2πk\) \(3x+\)\(\frac( π)(4)\) \(=-\)\(\frac(π)(2)\) \(+2πk\)

8) હંમેશની જેમ, આપણે સમીકરણોમાં \(x\) વ્યક્ત કરીશું.
સંખ્યાઓને \(π\), તેમજ \(1\), \(2\), \(\frac(1)(4)\), વગેરે સાથે વ્યવહાર કરવાનું ભૂલશો નહીં. આ બીજા બધાની સમાન સંખ્યાઓ છે. સંખ્યાત્મક ભેદભાવ નહીં!

\(3x=-\)\(\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=-\)\ (\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\)
\(3x=\)\(\frac(π)(4)\) \(+2πk\) \(|:3\) \(3x=-\)\(\frac(3π)(4)\) \(+2πk\) \(|:3\)
\(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\)

જવાબ: \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\), \(k∈Z\).

ત્રિકોણમિતિ સમીકરણોને સરળમાં ઘટાડવું એ એક સર્જનાત્મક કાર્ય છે; અહીં તમારે સમીકરણો ઉકેલવા માટે બંને અને વિશેષ પદ્ધતિઓનો ઉપયોગ કરવાની જરૂર છે:
- પદ્ધતિ (યુનિફાઇડ સ્ટેટ પરીક્ષામાં સૌથી વધુ લોકપ્રિય).
- પદ્ધતિ.
- સહાયક દલીલોની પદ્ધતિ.

ચાલો ચતુર્ભુજ ત્રિકોણમિતિ સમીકરણ ઉકેલવાના ઉદાહરણને ધ્યાનમાં લઈએ

ઉદાહરણ . ત્રિકોણમિતિ સમીકરણ ઉકેલો \(2\cos^2⁡x-5\cos⁡x+2=0\)
ઉકેલ:

\(2\cos^2⁡x-5\cos⁡x+2=0\)	ચાલો બદલીએ \(t=\cos⁡x\).

	આપણું સમીકરણ લાક્ષણિક બની ગયું છે. તમે તેનો ઉપયોગ કરીને હલ કરી શકો છો.
\(D=25-4 \cdot 2 \cdot 2=25-16=9\)
\(t_1=\)\(\frac(5-3)(4)\) \(=\)\(\frac(1)(2)\) ; \(t_2=\)\(\frac(5+3)(4)\) \(=2\)	અમે રિવર્સ રિપ્લેસમેન્ટ કરીએ છીએ.
\(\cos⁡x=\)\(\frac(1)(2)\); \(\cos⁡x=2\)	આપણે નંબર વર્તુળનો ઉપયોગ કરીને પ્રથમ સમીકરણ ઉકેલીએ છીએ. બીજા સમીકરણમાં કોઈ ઉકેલ નથી કારણ કે \(\cos⁡x∈[-1;1]\) અને કોઈપણ x માટે બે સમાન ન હોઈ શકે.
	ચાલો આ બિંદુઓ પર પડેલા તમામ નંબરો લખીએ.

જવાબ: \(x=±\)\(\frac(π)(3)\) \(+2πk\), \(k∈Z\).

ODZ ના અભ્યાસ સાથે ત્રિકોણમિતિ સમીકરણ ઉકેલવાનું ઉદાહરણ:

ઉદાહરણ (USE) . ત્રિકોણમિતિ સમીકરણ ઉકેલો \(=0\)

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	ત્યાં એક અપૂર્ણાંક છે અને એક કોટેન્જેન્ટ છે - તેનો અર્થ એ કે આપણે તેને લખવાની જરૂર છે. ચાલો હું તમને યાદ અપાવી દઉં કે કોટેન્જેન્ટ વાસ્તવમાં અપૂર્ણાંક છે: ctg\(x=\)\(\frac(\cos⁡x)(\sin⁡x)\) તેથી, ctg\(x\): \(\sin⁡x≠0\) માટે ODZ.
ODZ: ctg\(x ≠0\); \(\sin⁡x≠0\) \(x≠±\)\(\frac(π)(2)\) \(+2πk\); \(x≠πn\); \(k,n∈Z\)	ચાલો નંબર વર્તુળ પર "બિન-ઉકેલ" ને ચિહ્નિત કરીએ.

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	ચાલો સમીકરણમાંના છેદને ctg\(x\) વડે ગુણાકાર કરીને છૂટકારો મેળવીએ. અમે આ કરી શકીએ છીએ, કારણ કે અમે ઉપર લખ્યું છે કે ctg\(x ≠0\).
\(2\cos^2⁡x-\sin⁡(2x)=0\)	ચાલો સાઈન માટે ડબલ એંગલ ફોર્મ્યુલા લાગુ કરીએ: \(\sin⁡(2x)=2\sin⁡x\cos⁡x\).
\(2\cos^2⁡x-2\sin⁡x\cos⁡x=0\)	જો તમારા હાથ કોસાઇન દ્વારા વિભાજીત કરવા માટે પહોંચે છે, તો તેમને પાછા ખેંચો! તમે ચલ વડે અભિવ્યક્તિ દ્વારા ભાગી શકો છો જો તે ચોક્કસપણે શૂન્યની બરાબર ન હોય (ઉદાહરણ તરીકે, આ: \(x^2+1.5^x\)). તેના બદલે, ચાલો કૌંસમાંથી \(\cos⁡x\) લઈએ.
\(\cos⁡x (2\cos⁡x-2\sin⁡x)=0\)	ચાલો સમીકરણને બે ભાગમાં "વિભાજિત" કરીએ.
\(\cos⁡x=0\); \(2\cos⁡x-2\sin⁡x=0\)	ચાલો નંબર વર્તુળનો ઉપયોગ કરીને પ્રથમ સમીકરણ ઉકેલીએ. ચાલો બીજા સમીકરણને \(2\) વડે ભાગીએ અને \(\sin⁡x\) ને જમણી બાજુએ ખસેડીએ.

\(x=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\). \(\cos⁡x=\sin⁡x\)	પરિણામી મૂળ ODZ માં શામેલ નથી. તેથી, અમે તેમને જવાબમાં લખીશું નહીં. બીજું સમીકરણ લાક્ષણિક છે. ચાલો તેને \(\sin⁡x\) (\(\sin⁡x=0\) વડે ભાગીએ એ સમીકરણનો ઉકેલ હોઈ શકતો નથી કારણ કે આ કિસ્સામાં \(\cos⁡x=1\) અથવા \(\cos⁡ x=-1\)).
	અમે ફરીથી વર્તુળનો ઉપયોગ કરીએ છીએ.
\(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\)	આ મૂળ ODZ દ્વારા બાકાત નથી, તેથી તમે તેમને જવાબમાં લખી શકો છો.

જવાબ: \(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\).

cos સમીકરણ એક્સ = એ

સમીકરણનું દરેક મૂળ

cos એક્સ = એ (1)

સાઇનસૉઇડના કેટલાક આંતરછેદ બિંદુના એબ્સિસા તરીકે ગણી શકાય y = cosએક્સ સીધી રેખા સાથે y =એ , અને, તેનાથી વિપરિત, આવા દરેક આંતરછેદ બિંદુનો એબ્સીસા એ સમીકરણ (1) ના મૂળમાંથી એક છે. આમ, સમીકરણના તમામ મૂળનો સમૂહ (1) કોસાઇન તરંગના તમામ આંતરછેદ બિંદુઓના એબ્સીસાસના સમૂહ સાથે એકરુપ થાય છે. y = cosએક્સ સીધી રેખા સાથે y = એ .

જો | એ| >1 , પછી કોસાઇન y = cosએક્સ રેખા સાથે છેદે નથી y = એ .

આ કિસ્સામાં, સમીકરણ (1) ના કોઈ મૂળ નથી.

મુ |એ| < 1 આંતરછેદના અનંત ઘણા બિંદુઓ છે.

a > 0 માટે

એક માટે< 0.

અમે આ બધા આંતરછેદ બિંદુઓને બે જૂથોમાં વહેંચીશું:

A -2 , A - 1 , A 1 , A 2 , ... ,

બી -2 , બી - 1 , બી 1 , બી 2 , ... ,

ડોટ એએબ્સિસા છે આર્કોસ એ , અને પ્રથમ જૂથના અન્ય તમામ બિંદુઓ તેમાંથી 2 ના ગુણાંકના અંતરે અલગ પડે છે π

આર્કોસ a+ 2k π . (2)

ડોટ IN, જેમ કે આકૃતિઓથી સરળતાથી સમજી શકાય છે, તેમાં એબ્સીસા છે - આર્કોસએ , અને બીજા જૂથના અન્ય તમામ બિંદુઓ તેમાંથી 2 ના ગુણાંકના અંતરે દૂર કરવામાં આવે છે π . તેથી તેમના એબ્સિસાસ તરીકે વ્યક્ત કરવામાં આવે છે

આર્કોસ એ+ 2nπ . (3)

આમ, સમીકરણ (1) સૂત્રો (2) અને (3) દ્વારા વ્યાખ્યાયિત મૂળના બે જૂથો ધરાવે છે. પરંતુ આ બે સૂત્રો દેખીતી રીતે એક સૂત્ર તરીકે લખી શકાય છે

એક્સ = ± આર્કોસ a+ 2 મી π , (4)

જ્યાં mબધા પૂર્ણાંકો દ્વારા ચાલે છે (m = 0, ±1, ±2, ±3, ...).

આ સૂત્ર મેળવવામાં અમે જે તર્ક કર્યો છે તે સાચો છે તો જ
| a| =/= 1. જો કે, ઔપચારિક રીતે સંબંધ (4) સમીકરણના તમામ મૂળ નક્કી કરે છે cosx=a અને ખાતે | એ| =1. (તે સાબિત કરો!) તેથી આપણે કહી શકીએ કે સૂત્ર (4) કોઈપણ મૂલ્યો માટે સમીકરણ (1) ના તમામ મૂળ આપે છે એ , જો માત્ર |એ| < 1 .

પરંતુ હજુ પણ ત્રણ વિશેષ કિસ્સાઓમાં ( એ = 0, એ = -1, એ= +1) અમે સૂત્રનો ઉપયોગ ન કરવાની ભલામણ કરીએ છીએ (4) , પરંતુ અન્ય સંબંધોનો ઉપયોગ કરો. તે યાદ રાખવું ઉપયોગી છે કે સમીકરણના મૂળ cos એક્સ = 0 સૂત્ર દ્વારા આપવામાં આવે છે

એક્સ = π / 2 + એન π ; (5)

સમીકરણના મૂળ cos એક્સ = -1 સૂત્ર દ્વારા આપવામાં આવે છે

એક્સ = π + 2 મી π ; (6)

અને અંતે, સમીકરણના મૂળ cos એક્સ = 1 સૂત્ર દ્વારા આપવામાં આવે છે

એક્સ = 2 મી π ; (7)

નિષ્કર્ષમાં, અમે નોંધ કરીએ છીએ કે સૂત્રો (4) , (5), (6) અને (7) માત્ર ધારણા હેઠળ યોગ્ય છે કે ઇચ્છિત કોણ એક્સ રેડિયનમાં વ્યક્ત. જો તે ડિગ્રીમાં દર્શાવવામાં આવે છે, તો પછી આ સૂત્રોને કુદરતી રીતે બદલવાની જરૂર છે. તેથી, સૂત્ર (4) ફોર્મ્યુલા દ્વારા બદલવું જોઈએ

એક્સ = ± આર્કોસ a+ 360° n,

સૂત્ર (5) સૂત્ર

એક્સ = 90° + 180° nવગેરે