დახმარება Tele2-ზე, ტარიფები, კითხვები

ზახაროვა ლუდმილა ვლადიმეროვნა
MBOU „ბარნაულის No59 საშუალო სკოლა“.
მათემატიკის მასწავლებელი [ელფოსტა დაცულია]

№1 უმარტივესი ტრიგონომეტრიული განტოლებები

სამიზნე: 1. გამოიტანეთ ფორმის უმარტივესი ტრიგონომეტრიული განტოლებების ამონახსნების ფორმულები sinx =a, cosx=a, tgx=a, ctgx=a;

2. ისწავლეთ მარტივი ტრიგონომეტრიული განტოლებების ამოხსნა ფორმულების გამოყენებით.

აღჭურვილობა: 1) ცხრილები ტრიგონომეტრიული ფუნქციების გრაფიკებით y= sinx, y=cosx, y=tgx, y=ctgx; 2) შებრუნებული ტრიგონომეტრიული ფუნქციების მნიშვნელობების ცხრილი; 3) მარტივი ტრიგონომეტრიული განტოლებების ამოხსნის ფორმულების შემაჯამებელი ცხრილი.

ლექციის გაკვეთილის გეგმა:

1 .განტოლების ფესვების ფორმულების გამოყვანა

ა) სინქს =ა,

ბ) cosx= ა,

გ) tgx= ა,

დ) ctgx= ა.

2 . ზეპირი ფრონტალური მუშაობა მიღებული ფორმულების კონსოლიდაციის მიზნით.

3 . წერილობითი სამუშაო შესწავლილი მასალის კონსოლიდაციის მიზნით

გაკვეთილების დროს.

ალგებრაში, გეომეტრიაში, ფიზიკაში და სხვა საგნებში ჩვენ წინაშე ვდგავართ სხვადასხვა ამოცანების წინაშე, რომელთა ამოხსნა განტოლებების ამოხსნას გულისხმობს. ჩვენ შევისწავლეთ ტრიგონომეტრიული ფუნქციების თვისებები, ამიტომ ბუნებრივია მივმართოთ განტოლებებს, რომლებშიც უცნობი შედის ფუნქციის ნიშნის ქვეშ.

განმარტება: ფორმის განტოლებები სინქსი = ა , cosx= ა , tgx= ა , ctgx= ა უმარტივეს ტრიგონომეტრიულ განტოლებებს უწოდებენ.

ძალიან მნიშვნელოვანია ვისწავლოთ როგორ ამოხსნათ უმარტივესი ტრიგონომეტრიული განტოლებები, რადგან ნებისმიერი ტრიგონომეტრიული განტოლების ამოხსნის ყველა მეთოდი და ტექნიკა მოიცავს მათ უმარტივესამდე შემცირებას.

დავიწყოთ ფორმულების გამოყვანით, რომლებიც „აქტიურად“ მუშაობენ ტრიგონომეტრიული განტოლებების ამოხსნისას.

1.Sinx = ფორმის განტოლებები ა.

მოდით ამოხსნათ განტოლება sinx = აგრაფიკულად. ამისათვის ერთ კოორდინატულ სისტემაში ავაშენებთ y=sinx და y= ფუნქციების გრაფიკებს. ა.

1) თუ ა> 1 და აცოდვა x= აარ აქვს ამონახსნები, რადგან სწორ ხაზს და სინუს ტალღას არ აქვთ საერთო წერტილები.

2) თუ -1a a კვეთს სინუს ტალღას უსასრულოდ ბევრჯერ. ეს ნიშნავს, რომ განტოლება sinx= ააქვს უსაზღვროდ ბევრი გამოსავალი.

ვინაიდან სინუსის პერიოდი არის 2 , შემდეგ განტოლების ამოსახსნელად sinx= ასაკმარისია ყველა ამოხსნის პოვნა 2 სიგრძის ნებისმიერ სეგმენტზე.

განტოლების ამოხსნა [-/2-ზე; /2] რკალი x=-ის განმარტებითრკალი ადა x=-arcsin-ზე ა. у=sinx ფუნქციის პერიოდულობის გათვალისწინებით ვიღებთ შემდეგ გამონათქვამებს

x = -არცინი ა+2n, n Z.

გადაწყვეტილებების ორივე სერია შეიძლება გაერთიანდეს

X = (-1) n რკალი ა+n, nZ.

შემდეგ სამ შემთხვევაში, მათ ურჩევნიათ გამოიყენონ უფრო მარტივი ურთიერთობები, ვიდრე ზოგადი ფორმულა:

თუ ა=-1, შემდეგ sin x =-1, x=-/2+2n

თუ ა=1, შემდეგ sin x =1, x =/2+2n

თუ a= 0, შემდეგ sin x =0. x = n,

მაგალითი: ამოხსენით განტოლება sinx = 1/2.

მოდით შევქმნათ გადაწყვეტილებების ფორმულები x=arcsin 1/2+ 2n

X= - რკალი a+2n

მოდით გამოვთვალოთ ღირებულება arcsin1/2. მოდით შევცვალოთ ნაპოვნი მნიშვნელობა ამოხსნის ფორმულებში

x=5/6+2 n

ან ზოგადი ფორმულის მიხედვით

X= (-1) n რკალი 1/2+n,

X= (-1) n /6+n,

2. ფორმის განტოლებები cosx= ა.

ამოვიხსნათ განტოლება cosx= აასევე გრაფიკულად, y= cosx და y= ფუნქციების გამოსახვით ა.

1) თუ a 1, მაშინ განტოლება cosx= აარ აქვს ამონახსნები, რადგან გრაფიკებს არ აქვთ საერთო წერტილები.

2) თუ -1 ა cosx= ააქვს ამონახსნების უსასრულო რაოდენობა.

ჩვენ ვიპოვით ყველა გამოსავალს cosx= ა 2 სიგრძის ინტერვალზე, ვინაიდან კოსინუსის პერიოდი არის 2.

რკალის კოსინუსის განმარტებით, განტოლების ამონახსნი იქნება x=არკოსი ა. კოსინუსური ფუნქციის პარიტეტის გათვალისწინებით, [-;0] განტოლების ამონახსნი იქნება x=-arcos. ა.

ამრიგად, განტოლების ამოხსნა cosx= ა x= + არკოსები ა+ 2 n,

სამ შემთხვევაში, ჩვენ არ გამოვიყენებთ ზოგად ფორმულას, არამედ უფრო მარტივ ურთიერთობებს:

თუ ა=-1, შემდეგ cosx =-1, x =-/2+2n

თუ ა=1, შემდეგ cosx =1, x = 2n,

თუ a=0, მაშინ cosx=0. x =/2+n

მაგალითი: ამოხსენით განტოლება cos x =1/2,

მოდით შევქმნათ გადაწყვეტილებების ფორმულები x=arccos 1/2+ 2n

მოდით გამოვთვალოთ ღირებულება arccos1/2.

მოდით შევცვალოთ ნაპოვნი მნიშვნელობა ამოხსნის ფორმულებში

X= + /3+ 2n, nZ.

ფორმის განტოლებები tgx= ა.

ვინაიდან ტანგენტის პერიოდი ტოლია, მაშინ განტოლების ყველა ამონახსნის პოვნა tgx= ასაკმარისია ყველა ამონახსნის პოვნა სიგრძის ნებისმიერ ინტერვალზე . არქტანგენტის განმარტებით, (-/2; /2) განტოლების ამონახსნი არის არქტანი ა. ფუნქციის პერიოდის გათვალისწინებით, განტოლების ყველა ამონახსნი შეიძლება ჩაიწეროს ფორმით

x= არქტანი ა+ n, nZ.

მაგალითი:ამოხსენით განტოლება tan x = 3/3

შევქმნათ x=-ის ამოხსნის ფორმულაარქტანი 3/3 +n, nZ.

გამოვთვალოთ არქტანგენტის მნიშვნელობაარქტანი 3/3= /6, მაშინ

X=/6+ n, nZ.

განტოლების ამოხსნის ფორმულის გამოყვანა თან tgx= აშეიძლება მიეწოდოს სტუდენტებს.

მაგალითი.

ამოხსენით განტოლება ctg x = 1.

x = arcсtg 1 + n, nZ,

X = /4 + n, nZ.

შესწავლილი მასალის შედეგად მოსწავლეებს შეუძლიათ შეავსონ ცხრილი:

"ტრიგონომეტრიული განტოლებების ამოხსნა".

განტოლება

სავარჯიშოები შესწავლილი მასალის კონსოლიდაციის მიზნით.

(ზეპირი) წერილობითი განტოლებიდან რომელი ამოხსნილია ფორმულების გამოყენებით:

ა) x= (-1) n რკალი ა+n, nZ;

ბ) x= + არკოსები a+ 2 n?

cos x = 2/2, tan x= 1, sin x = 1/3, cos x = 3/3, sin x = -1/2, cos x= 2/3, sin x = 3, cos x = 2 .

ჩამოთვლილი განტოლებიდან რომელს არ აქვს ამონახსნები?

ამოხსენით განტოლებები:

ა) sin x = 0; ე) sin x = 2/2; თ) sin x = 2;

ბ) cos x = 2/2; ე) cos x = -1/2; ი) cos x = 1;

დ) თან x = 3; ზ) საწოლი x = -1; კ) თან x = 1/3.

3. ამოხსენით განტოლებები:

ა) ცოდვა 3x = 0; ე) 2cos x = 1;

ბ) cos x/2 =1/2; ე) 3 ტგ 3x =1;

დ) ცოდვა x/4 = 1; ზ) 2cos(2x+ /5) = 3.

ამ განტოლებების ამოხსნისას სასარგებლოა ფორმის განტოლებების ამოხსნის წესების ჩაწერაცოდვა ვ x = ა, და თანცოდვა ვ x = ა, | ა|1.

ცოდვა ვ x = ა, |ა|1.

ვ x = (-1) n რკალი ა+n, nZ,

x= (-1) n 1/ ვრკალი ა+n/ ვ, nZ.

გაკვეთილის შეჯამება:

დღეს კლასში გამოვიყვანეთ მარტივი ტრიგონომეტრიული განტოლებების ამოხსნის ფორმულები.

ჩვენ ვიხილეთ მარტივი ტრიგონომეტრიული განტოლებების ამოხსნის მაგალითები.

შევავსეთ ცხრილი, რომელსაც გამოვიყენებთ განტოლებების ამოსახსნელად.

Საშინაო დავალება.

№2 ტრიგონომეტრიული განტოლებების ამოხსნა

სამიზნე: ტრიგონომეტრიული განტოლებების ამოხსნის კვლევის მეთოდები: 1) რედუცირებადი კვადრატულამდე, 2) რედუცირებადი ერთგვაროვან ტრიგონომეტრიულ განტოლებამდე.

ტრიგონომეტრიული განტოლებების ამოხსნის სხვადასხვა მეთოდის გამოყენებისას მოსწავლეთა დაკვირვების უნარის განვითარება.

ფრონტალური მუშაობა მოსწავლეებთან.

როგორია ტრიგონომეტრიული განტოლებების ფესვების ფორმულები? cos x= ა, ცოდვა x= ა, tgx = ა, ctg x = ა.

ამოხსენით განტოლებები (ზეპირად):

cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1.5, sin x=0.

იპოვნეთ შეცდომები და იფიქრეთ შეცდომების მიზეზებზე.

cos x=1/2, x= + /6+2k,k ზ.

sin x= 3/2, x= /3+k, kZ.

tgx = /4, x=1+ k, kZ.

2. ახალი მასალის შესწავლა.

ეს გაკვეთილი მოიცავს ტრიგონომეტრიული განტოლებების ამოხსნის ყველაზე გავრცელებულ მეთოდებს.

ტრიგონომეტრიული განტოლებები დაყვანილია კვადრატამდე.

ეს კლასი შეიძლება შეიცავდეს განტოლებებს, რომლებიც შეიცავენ ერთ ფუნქციას (სინუსს ან კოსინუსს) ან ერთი და იმავე არგუმენტის ორ ფუნქციას, მაგრამ ერთი მათგანი მცირდება მეორეზე ძირითადი ტრიგონომეტრიული იდენტობების გამოყენებით.

მაგალითად, თუ cosх განტოლებაში შედის ლუწი ხარისხებით, მაშინ მას ვცვლით 1-sin 2 x, თუ sin 2 x, მაშინ ვცვლით 1-cos 2 x-ით.

მაგალითი.

ამოხსენით განტოლება: 8 sin 2 x - 6sin x -5 =0.

ამოხსნა: აღვნიშნოთ sin x=t, შემდეგ 8t 2 - 6t – 5=0,

D = 196,

T 1 = -1/2, t 2 = -5/4.

შევასრულოთ საპირისპირო ჩანაცვლება და ამოხსნათ შემდეგი განტოლებები.

X=(-1) k+1 /6+ k, kZ.

ვინაიდან -5/4>1, განტოლებას არ აქვს ფესვები.

პასუხი: x=(-1) k+1 /6+ k, kZ.

კონსოლიდაციის სავარჯიშოების ამოხსნა.

ამოხსენით განტოლება:

1) 2sin 2 x+ 3cos x = 0;

2) 5sin 2 x+ 6cos x -6 = 0;

3) 2sin 2 x+ 3cos 2 x = -2sin x;

4) 3 tg 2 x +2 tgx-1=0.

ჰომოგენური ტრიგონომეტრიული განტოლებები.

განმარტება: 1) ფორმის განტოლებაა სინქსი + ბ cosx=0, (a=0, b=0)ეწოდება პირველი ხარისხის ერთგვაროვანი განტოლება sin x და cos x მიმართ.

ეს განტოლება წყდება ორივე მხარის გაყოფით cosx 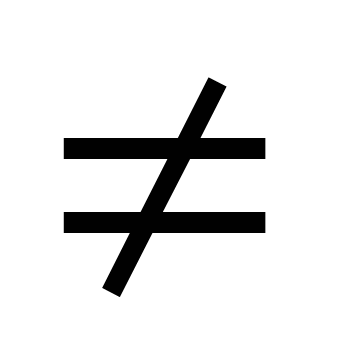0. შედეგი არის განტოლება atgx+ b=0.

2) ფორმის განტოლებაა ცოდვა 2 x + ბ სინქსი cosx + გ cos 2 x =0 ეწოდება მეორე ხარისხის ერთგვაროვან განტოლებას, სადაც a, b, c არის ნებისმიერი რიცხვი.

თუ a = 0, მაშინ განტოლებას ვხსნით ორივე მხარის გაყოფით cos 2 x 0. შედეგად ვიღებთ განტოლებას atg 2 x+ btgx+с =0.

კომენტარი:ფორმის განტოლებაა ცოდვა mx + ბ cos mx=0 ან

ა ცოდვა 2 mx + ბ ცოდვა mx cos mx + გ cos 2 mx =0 ასევე ერთგვაროვანია. მათი ამოსახსნელად, განტოლების ორივე მხარე იყოფა co-ზე mx=0 ან co 2 mx=0

3) სხვადასხვა განტოლებები, რომლებიც თავდაპირველად არ არის ერთგვაროვანი განტოლებები, შეიძლება შემცირდეს ერთგვაროვან განტოლებამდე. Მაგალითად,ცოდვა 2 mx + ბ ცოდვა mx cos mx + გ cos 2 mx = დ, და ა სინქსი + ბ cosx= დ. ამ განტოლებების ამოსახსნელად საჭიროა მარჯვენა მხარის გამრავლება "ტრიგონომეტრიული ერთეული"იმათ. on ცოდვა 2 x + cos 2 xდა შეასრულოს მათემატიკური გარდაქმნები.

სავარჯიშოები შესწავლილი მასალის კონსოლიდაციისთვის:

1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;

2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;

3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;

4) sin 2 x -3 sinx cosx +2 cos 2 x =0

3. გაკვეთილის შეჯამება. Საშინაო დავალება.

ამ გაკვეთილზე, ჯგუფის მზადყოფნის მიხედვით, შეგიძლიათ განიხილოთ ფორმის განტოლებების ამოხსნა a sin mx +b cos mx=c, სადაც a, b, c ერთდროულად ნულის ტოლი არ არის.

გამაძლიერებელი ვარჯიშები:

1. 3sin x + cos x=2;

2. 3sin 2x + cos 2x= 2;

3. sin x/3 + cos x/3=1;

4. 12 sin x +5 cos x+13=0.

№ 3 ტრიგონომეტრიული განტოლებების ამოხსნა

სამიზნე: 1) ტრიგონომეტრიული განტოლებების ფაქტორიზაციით ამოხსნის მეთოდის შესწავლა; ისწავლოს ტრიგონომეტრიული განტოლებების ამოხსნა სხვადასხვა ტრიგონომეტრიული ფორმულების გამოყენებით;

2) შეამოწმეთ: მოსწავლეთა ცოდნა მარტივი ტრიგონომეტრიული განტოლებების ამოხსნის ფორმულების შესახებ; მარტივი ტრიგონომეტრიული განტოლებების ამოხსნის უნარი.

Გაკვეთილის გეგმა:

საშინაო დავალების შემოწმება.

მათემატიკური კარნახი.

ახალი მასალის სწავლა.

დამოუკიდებელი მუშაობა.

გაკვეთილის შეჯამება. Საშინაო დავალება.

გაკვეთილის მიმდინარეობა:

საშინაო დავალების შემოწმება (ტრიგონომეტრიული განტოლებების ამონახსნები მოკლედ იწერება დაფაზე).

მათემატიკური კარნახი.

1-ში

1. რომელ განტოლებებს უწოდებენ უმარტივეს ტრიგონომეტრიულ განტოლებებს?

2. რა ჰქვია ფორმის განტოლებასა sinx + ბ cosx=0? მიუთითეთ მისი გადაჭრის გზა.

3.ჩაწერეთ განტოლების ფესვების ფორმულა tgx = ა(ctg x= ა).

4. ჩამოწერეთ ფორმის განტოლების ფესვების ფორმულები cosx= ა, სად ა=1, ა=0, ა=-1.

5. ჩამოწერეთ განტოლების ფესვების ზოგადი ფორმულაცოდვა x= ა, | ა|

6. როგორ იხსნება ფორმის განტოლებებია cosx= ბ, | ბ|

2-ზე

1. ჩამოწერეთ განტოლებათა ფესვების ფორმულები cosx= ა,| ა|

2. ჩამოწერეთ განტოლების ფესვების ზოგადი ფორმულა

= ა, | ა|

3. რა ჰქვია ფორმის განტოლებებს?ცოდვა x= ა, tgx = ა, ცოდვა x= ა?

4.ჩაწერეთ განტოლების ფესვების ფორმულებიცოდვა x= ა, თუ ა=1, ა=0, ა=-1.

5. როგორ იხსნება ფორმის განტოლებებიცოდვა ა x= ბ, | ბ|

6. რომელ განტოლებებს უწოდებენ მეორე ხარისხის ერთგვაროვან განტოლებებს? როგორ წყდება ისინი?

ახალი მასალის სწავლა.

ფაქტორიზაციის მეთოდი.

ტრიგონომეტრიული განტოლებების ამოხსნის ერთ-ერთი ყველაზე ხშირად გამოყენებული მეთოდია ფაქტორილიზაციის მეთოდი.

თუ განტოლება f(x) =0 შეიძლება წარმოდგენილი იყოს როგორც f 1 (x) f 2 (x) =0, მაშინ ამოცანა მცირდება ორი განტოლების ამოხსნამდე f 1 (x) = 0, f 2 (x) = 0. .

(მოსწავლეებთან ერთად სასარგებლოა გახსოვდეთ წესი " ფაქტორების ნამრავლი ნულის ტოლია, თუ ფაქტორებიდან ერთი მაინც ნულის ტოლია, ხოლო დანარჩენებს აქვთ აზრი»)

შესწავლილი მასალის კონსოლიდაცია სხვადასხვა სირთულის განტოლებების ამოხსნის გზით.

(ცოდვა x-1/2)(ცოდვა x+1)=0; 2) (cosx- 2/2)(ცოდვა x+ 2/2)=0;(თვითონ)

3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;

5) sin 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2 გზა)

7) cosx+ cos3x=0; 8) ცოდვა 3x= ცოდვა 17x;

9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x

11) sin x cos5x = sin 9x cos3x sin 2x sin 2x

12) 3 cosx sin x+ cos 2 x=0(თვითონ)

13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.

დამოუკიდებელი მუშაობა.

ვარიანტი-1 ვარიანტი-2

1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;

2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;

3) 5 sin 2 x+ sin x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5;

4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;

5) sin x+cosx=1. 5) sin x+cosx=2.

8. გაკვეთილის შეჯამება. Საშინაო დავალება.

გაკვეთილის ტიპი:სასწავლო დავალების დაყენება.

გაკვეთილის მიზნები:

საგანმანათლებლო: მოსწავლეთა ცოდნის სისტემატიზაცია მარტივი ტრიგონომეტრიული განტოლებების ამოხსნის მეთოდების შესახებ, წრეებთან და ცხრილებთან მუშაობის უნარების კონსოლიდაცია.

განმავითარებელი: გააგრძელეთ მუშაობა მოსწავლეთა შემოქმედებითი ინტელექტუალური შესაძლებლობების ფორმირებაზე ტრიგონომეტრიული განტოლებების ამოხსნის სხვადასხვა ტექნიკის გამოყენებით.

საგანმანათლებლო: განუვითარდებათ კოლექტიური გონებრივი აქტივობის, ურთიერთდახმარებისა და საკუთარისაგან განსხვავებული თვალსაზრისის მიღების უნარები.

გაკვეთილების დროს

1. წარმატების მდგომარეობა.

ამოხსენით განტოლება: cosx=1; cosx=0; cosx= -1.

2. სიტუაცია, უფსკრული” ცოდნასა და უცოდინრობას შორის.

ამოხსენით განტოლება: cosx=½; cosx=a.

დისკუსია.

3. განცხადება სასწავლო დავალების შესახებ.

როგორ ამოხსნათ ამ ტიპის განტოლება?

1) რა უდრის წერტილის აბსცისა ერთეულ წრეზე, რომელიც მიღებულია წერტილის (1;0) საწყის ირგვლივ ტოლი კუთხით ბრუნვით: ?

2). რას უდრის: ?

პასუხი:

3).რისი ტოლია: .

პასუხი:

;

;

(1) .

მასწავლებლის სიტყვები: მათემატიკოსებმა სიტყვებს reverse cos უწოდეს „სიტყვა არკოზინი. რიცხვის რკალის კოსინუსი არის რიცხვი, რომლის კოსინუსი უდრის a-ს:
arccosa=α,თუ cosα=a და 0≤α≤π.

4). დაწერეთ ტოლობა (1) arccos სიმბოლოს გამოყენებით.

5). ამოხსენით განტოლებები: cosx=½, cosx=α.

პასუხი: x=arccos½, x=arccosa.

6). დაასახელეთ ½-ის ტოლი აბსცისის მქონე ერთეული წრის (1;0) წერტილის ბრუნვის კუთხეები.

პასუხი: აბსცისა უდრის ½-ს, როდესაც წერტილი ბრუნავს π/3 და -π/3 ტოლი კუთხით.

ანუ cosx=½ x=±arccos½-ზე
cosx=a x=±arccosa-ზე.

7). როგორია წერტილის (1;0) კუთხით მობრუნებით მიღებული წერტილების აბსცისები: π/3+2π; π/3+6π; -π/3+4π; -π/3+8π; π/3+2πn; -π/3+2πn.

პასუხი: აბსცისა არის ½ და cosx=½ x=±arccos½+2πn,.
cosx=a x=±arccosa+2πn,.

8). დასკვნა: განტოლება cosx=a

1) აქვს ფესვები, თუ ≤1,
2) არ აქვს ფესვები, თუ >1.

9). გაკვეთილის შეჯამება:

ა) a და α-ს რა მნიშვნელობებისთვის აქვს აზრი ტოლობას arccosa = α?
ბ) რას ეწოდება a-ს რკალის კოსინუსი?
გ) a-ს რომელ მნიშვნელობებზე აქვს ფესვები cosx=a განტოლებას?
დ) cosx=a განტოლების ფესვების მოძიების ფორმულა.

უმარტივესი ტრიგონომეტრიული განტოლებები არის განტოლებები

Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) =a

განტოლება cos(x) = a

ახსნა და დასაბუთება

1. განტოლების ფესვები cosx = a. როდის | a | > 1 განტოლებას არ აქვს ფესვები, ვინაიდან | cosx |< 1 для любого x (прямая y = а при а >1 ან ა< -1 не пересекает график функцииy = cosx).

მოდით | a |< 1. Тогда прямая у = а пересекает график функции

y = cos x. ინტერვალზე ფუნქცია y = cos x მცირდება 1-დან -1-მდე. მაგრამ კლებადი ფუნქცია იღებს მის თითოეულ მნიშვნელობას მხოლოდ მისი განსაზღვრის დომენის ერთ წერტილში, ამიტომ განტოლებას cos x = a აქვს მხოლოდ ერთი ფესვი ამ ინტერვალზე, რომელიც, არკოზინის განმარტებით, უდრის: x 1 = arccos a (და ამ ფესვისთვის cos x = A).

კოსინუსი არის ლუწი ფუნქცია, ასე რომ [-n; 0] განტოლება cos x = და ასევე აქვს მხოლოდ ერთი ფესვი - რიცხვი საპირისპირო x 1, ანუ

x 2 = -arccos a.

ამრიგად, ინტერვალზე [-n; p] (სიგრძე 2p) განტოლება cos x = a | a |< 1 имеет только корни x = ±arccos а.

ფუნქცია y = cos x პერიოდულია 2n პერიოდით, ამიტომ ყველა სხვა ფესვი განსხვავდება 2n-ით ნაპოვნი ფესვებისგან (n € Z). ჩვენ ვიღებთ შემდეგ ფორმულას განტოლების ფესვებისთვის cos x = a როდესაც

x = ±arccos a + 2pp, n £ Z.

1. განტოლების ამოხსნის სპეციალური შემთხვევები cosx = a.

სასარგებლოა დამახსოვრება სპეციალური აღნიშვნები განტოლების ფესვებისთვის cos x = a when

a = 0, a = -1, a = 1, რომელიც ადვილად მიიღება ერთეული წრის გამოყენებით, როგორც მითითება.

ვინაიდან კოსინუსი ტოლია ერთეული წრის შესაბამისი წერტილის აბსცისა, მივიღებთ cos x = 0 თუ და მხოლოდ იმ შემთხვევაში, თუ ერთეული წრის შესაბამისი წერტილი არის A წერტილი ან წერტილი B.

ანალოგიურად, cos x = 1 თუ და მხოლოდ იმ შემთხვევაში, თუ ერთეული წრის შესაბამისი წერტილი არის წერტილი C, შესაბამისად,

x = 2πп, k € Z.

ასევე cos x = -1 თუ და მხოლოდ იმ შემთხვევაში, თუ ერთეული წრის შესაბამისი წერტილი არის წერტილი D, შესაბამისად x = n + 2n,

განტოლება sin(x) = a

ახსნა და დასაბუთება

1. განტოლების ფესვები sinx = a. როდის | a | > 1 განტოლებას არ აქვს ფესვები, ვინაიდან | sinx |< 1 для любого x (прямая y = а на рисунке при а >1 ან ა< -1 не пересекает график функции y = sinx).

მაგალითები:

\(2\sin(⁡x) = \sqrt(3)\)
tg\((3x)=-\) \(\frac(1)(\sqrt(3))\)
\(4\cos^2⁡x+4\sin⁡x-1=0\)
\(\cos⁡4x+3\cos⁡2x=1\)

როგორ ამოხსნათ ტრიგონომეტრიული განტოლებები:

ნებისმიერი ტრიგონომეტრიული განტოლება უნდა შემცირდეს ერთ-ერთ შემდეგ ტიპზე:

\(\sin⁡t=a\), \(\cos⁡t=a\), tg\(t=a\), ctg\(t=a\)

სადაც \(t\) არის გამოხატულება x-ით, \(a\) არის რიცხვი. ასეთ ტრიგონომეტრიულ განტოლებებს ე.წ უმარტივესი. მათი მარტივად გადაჭრა შესაძლებელია () ან სპეციალური ფორმულების გამოყენებით:

იხილეთ ინფოგრაფიკა მარტივი ტრიგონომეტრიული განტოლებების ამოხსნის შესახებ აქ:, და.

მაგალითი . ამოხსენით ტრიგონომეტრიული განტოლება \(\sin⁡x=-\)\(\frac(1)(2)\).
გამოსავალი:

პასუხი: \(\მარცხნივ[ \დაწყება(შეიკრიბა)x=-\frac(π)(6)+2πk, \\ x=-\frac(5π)(6)+2πn, \ბოლო(შეიკრიბა)\მარჯვნივ.\) \(k,n∈Z\)

რას ნიშნავს თითოეული სიმბოლო ტრიგონომეტრიული განტოლებების ფესვების ფორმულაში, იხ.

ყურადღება!განტოლებებს \(\sin⁡x=a\) და \(\cos⁡x=a\) არ აქვთ ამონახსნები, თუ \(a ϵ (-∞;-1)∪(1;∞)\). რადგან ნებისმიერი x-სთვის სინუსი და კოსინუსი მეტია ან ტოლია \(-1\) და ნაკლები ან ტოლი \(1\):

\(-1≤\sin x≤1\) \(-1≤\cos⁡x≤1\)

მაგალითი . ამოხსენით განტოლება \(\cos⁡x=-1,1\).
გამოსავალი: \(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
უპასუხე : გადაწყვეტილებები არ არის.

მაგალითი . ამოხსენით ტრიგონომეტრიული განტოლება tg\(⁡x=1\).
გამოსავალი:

მოდით ამოხსნათ განტოლება რიცხვითი წრის გამოყენებით. Ამისთვის: 1) შექმენით წრე) 2) ააგეთ ღერძები \(x\) და \(y\) და ტანგენსი ღერძი (ის გადის \((0;1)\) ღერძის პარალელურად \(y\) წერტილს). 3) ტანგენტის ღერძზე მონიშნეთ წერტილი \(1\). 4) დააკავშირეთ ეს წერტილი და კოორდინატების საწყისი - სწორი ხაზი. 5) მონიშნეთ ამ წრფის გადაკვეთის წერტილები და რიცხვითი წრე. 6) მოვაწეროთ ხელი ამ წერტილების მნიშვნელობებს: \(\frac(π)(4)\) ,\(\frac(5π)(4)\) 7) ჩაწერეთ ამ წერტილების ყველა მნიშვნელობა. ვინაიდან ისინი განლაგებულია ერთმანეთისგან ზუსტად \(π\) მანძილზე, ყველა მნიშვნელობა შეიძლება ჩაიწეროს ერთ ფორმულაში:

პასუხი: \(x=\)\(\frac(π)(4)\) \(+πk\), \(k∈Z\).

მაგალითი . ამოხსენით ტრიგონომეტრიული განტოლება \(\cos⁡(3x+\frac(π)(4))=0\).
გამოსავალი:

ისევ გამოვიყენოთ რიცხვითი წრე. 1) ააგეთ წრე, ღერძები \(x\) და \(y\). 2) კოსინუსის ღერძზე (\(x\) ღერძი), მონიშნეთ \(0\). 3) ამ წერტილის გავლით კოსინუსის ღერძის პერპენდიკულარული დახაზვა. 4) მონიშნეთ პერპენდიკულარულისა და წრის გადაკვეთის წერტილები. 5) მოვაწეროთ ხელი ამ წერტილების მნიშვნელობებს: \(-\) \(\frac(π)(2)\),\(\frac(π)(2)\). 6) ჩვენ ვწერთ ამ წერტილების მთელ მნიშვნელობას და ვაიგივებთ მათ კოსინუსთან (რაც არის კოსინუსში). \(3x+\)\(\frac(π)(4)\) \(=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\) \(3x+\)\(\frac(π)(4)\) \(=\)\(\frac(π)(2)\) \(+2πk\) \(3x+\)\(\frac( π)(4)\) \(=-\)\(\frac(π)(2)\) \(+2πk\) 8) ჩვეულებისამებრ, ჩვენ გამოვხატავთ \(x\) განტოლებებს. არ დაგავიწყდეთ რიცხვების დამუშავება \(π\), ასევე \(1\), \(2\), \(\frac(1)(4)\) და ა.შ. ეს იგივე რიცხვებია, როგორც ყველა სხვა. არანაირი რიცხვითი დისკრიმინაცია! \(3x=-\)\(\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=-\)\ (\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=\)\(\frac(π)(4)\) \(+2πk\) \(|:3\) \(3x=-\)\(\frac(3π)(4)\) \(+2πk\) \(|:3\) \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\)

პასუხი: \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\) , \(k∈Z\).

ტრიგონომეტრიული განტოლებების უმარტივესამდე შემცირება შემოქმედებითი ამოცანაა; აქ თქვენ უნდა გამოიყენოთ ორივე და სპეციალური მეთოდები განტოლებების გადასაჭრელად:
- მეთოდი (ყველაზე პოპულარული ერთიან სახელმწიფო გამოცდაში).
- მეთოდი.
- დამხმარე არგუმენტების მეთოდი.

განვიხილოთ კვადრატული ტრიგონომეტრიული განტოლების ამოხსნის მაგალითი

მაგალითი . ამოხსენით ტრიგონომეტრიული განტოლება \(2\cos^2⁡x-5\cos⁡x+2=0\)
გამოსავალი:

\(2\cos^2⁡x-5\cos⁡x+2=0\)	მოდით გავაკეთოთ ჩანაცვლება \(t=\cos⁡x\).
	ჩვენი განტოლება გახდა ტიპიური. თქვენ შეგიძლიათ მისი გადაჭრა გამოყენებით.
\(D=25-4 \cdot 2 \cdot 2=25-16=9\)
\(t_1=\)\(\frac(5-3)(4)\) \(=\)\(\frac(1)(2)\) ; \(t_2=\)\(\frac(5+3)(4)\) \(=2\)	ჩვენ ვაკეთებთ საპირისპირო ჩანაცვლებას.
\(\cos⁡x=\)\(\frac(1)(2)\); \(\cos⁡x=2\)	პირველ განტოლებას ვხსნით რიცხვითი წრის გამოყენებით. მეორე განტოლებას არ აქვს ამონახსნები, რადგან \(\cos⁡x∈[-1;1]\) და არ შეიძლება იყოს ორის ტოლი ნებისმიერი x-ისთვის.
	მოდით ჩამოვწეროთ ამ წერტილებში მყოფი ყველა რიცხვი.

პასუხი: \(x=±\)\(\frac(π)(3)\) \(+2πk\), \(k∈Z\).

ტრიგონომეტრიული განტოლების ამოხსნის მაგალითი ODZ-ის შესწავლით:

მაგალითი (USE) . ამოხსენით ტრიგონომეტრიული განტოლება \(=0\)

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	არის წილადი და არის კოტანგენსი - ეს ნიშნავს, რომ უნდა ჩავწეროთ. შეგახსენებთ, რომ კოტანგენსი სინამდვილეში არის წილადი: ctg\(x=\)\(\frac(\cos⁡x)(\sin⁡x)\) ამიტომ, ODZ ctg\(x\): \(\sin⁡x≠0\).
ODZ: ctg\(x ≠0\); \(\sin⁡x≠0\) \(x≠±\)\(\frac(π)(2)\) \(+2πk\); \(x≠πn\); \(k,n∈Z\)	რიცხვთა წრეზე მოვნიშნოთ „არაამოხსნა“.
\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	მოდი, გავთავისუფლდეთ განტოლების მნიშვნელს ctg\(x\)-ზე გამრავლებით. ჩვენ შეგვიძლია ამის გაკეთება, რადგან ზემოთ დავწერეთ, რომ ctg\(x ≠0\).
\(2\cos^2⁡x-\sin⁡(2x)=0\)	გამოვიყენოთ ორმაგი კუთხის ფორმულა სინუსისთვის: \(\sin⁡(2x)=2\sin⁡x\cos⁡x\).
\(2\cos^2⁡x-2\sin⁡x\cos⁡x=0\)	თუ თქვენი ხელები კოსინუსზე გასაყოფად გაიწელეთ, უკან დაიხიეთ! თქვენ შეგიძლიათ გაყოთ გამოხატულებაზე ცვლადით, თუ ის ნამდვილად არ არის ნულის ტოლი (მაგალითად, ეს: \(x^2+1.5^x\)). ამის ნაცვლად, ავიღოთ \(\cos⁡x\) ფრჩხილებიდან.
\(\cos⁡x (2\cos⁡x-2\sin⁡x)=0\)	მოდით "გავყოთ" განტოლება ორად.
\(\cos⁡x=0\); \(2\cos⁡x-2\sin⁡x=0\)	პირველი განტოლება გადავწყვიტოთ რიცხვითი წრის გამოყენებით. მოდით გავყოთ მეორე განტოლება \(2\)-ზე და გადავიტანოთ \(\sin⁡x\) მარჯვენა მხარეს.
\(x=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\). \(\cos⁡x=\sin⁡x\)	შედეგად ფესვები არ შედის ODZ-ში. ამიტომ მათ პასუხად არ ჩამოვწერთ. მეორე განტოლება ტიპიურია. მოდით გავყოთ \(\sin⁡x\)-ზე (\(\sin⁡x=0\) არ შეიძლება იყოს განტოლების ამონახსნი, რადგან ამ შემთხვევაში \(\cos⁡x=1\) ან \(\cos⁡ x=-1\)).
	ჩვენ კვლავ ვიყენებთ წრეს.
\(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\)	ეს ფესვები არ არის გამორიცხული ODZ-ის მიერ, ასე რომ თქვენ შეგიძლიათ დაწეროთ ისინი პასუხში.

პასუხი: \(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\).

cos განტოლება X = ა

განტოლების თითოეული ფესვი

cos X = ა (1)

შეიძლება ჩაითვალოს სინუსოიდის რომელიმე გადაკვეთის წერტილის აბსცისად y = cosX სწორი ხაზით y =ა და, პირიქით, თითოეული ასეთი გადაკვეთის წერტილის აბსცისა არის (1) განტოლების ერთ-ერთი ფესვი. ამრიგად, (1) განტოლების ყველა ფესვების სიმრავლე ემთხვევა კოსინუსური ტალღის ყველა გადაკვეთის წერტილის აბსცისების სიმრავლეს. y = cosX სწორი ხაზით y = ა .

თუ | ა| >1 , შემდეგ კოსინუსი y = cosX არ კვეთს ხაზს y = ა .

ამ შემთხვევაში, განტოლებას (1) არ აქვს ფესვები.

ზე |ა| < 1 გადაკვეთის უსასრულოდ ბევრი წერტილია.

> 0-ისთვის

თვის< 0.

ყველა ამ გადაკვეთის წერტილს ორ ჯგუფად გავყოფთ:

A -2 , A - 1 , A 1 , A 2 , ... ,

B -2 , B - 1 , B 1 , B 2 , ... ,

Წერტილი ააქვს აბსციზა არკოები ა და პირველი ჯგუფის ყველა სხვა წერტილი მისგან გამოყოფილია 2-ის ჯერადი მანძილით π

არკოები ა+ 2 კ π . (2)

Წერტილი INროგორც ფიგურებიდან ადვილად გასაგებია, აქვს აბსციზა - რკალებია და მეორე ჯგუფის ყველა სხვა წერტილი ამოღებულია მისგან 2-ის ჯერადი დისტანციებზე π . ამიტომ მათი აბსციები გამოიხატება როგორც

არკოები ა+ 2nπ . (3)

ამრიგად, განტოლებას (1) აქვს ფესვების ორი ჯგუფი, რომლებიც განსაზღვრულია (2) და (3) ფორმულებით. მაგრამ ეს ორი ფორმულა აშკარად შეიძლება დაიწეროს როგორც ერთი ფორმულა

X = ± რკალი ა+ 2 მ π , (4)

სად მგადის ყველა მთელ რიცხვში (m = 0, ±1, ±2, ±3, ...).

მსჯელობა, რომელიც ჩვენ განვახორციელეთ ამ ფორმულის გამოყვანისას სწორია მხოლოდ იმ შემთხვევაში, თუ
| ა| =/= 1. თუმცა, ფორმალურად მიმართება (4) განსაზღვრავს განტოლების ყველა ფესვს cosx=a და | ა| =1. (დაამტკიცე!) ამიტომ შეგვიძლია ვთქვათ, რომ ფორმულა (4) იძლევა (1) განტოლების ყველა ფესვს ნებისმიერი მნიშვნელობისთვის ა , თუ მხოლოდ |ა| < 1 .

მაგრამ მაინც სამ განსაკუთრებულ შემთხვევაში ( ა = 0, ა = -1, ა= +1) ჩვენ გირჩევთ არ გამოიყენოთ ფორმულა (4) , მაგრამ გამოიყენეთ სხვა ურთიერთობები. სასარგებლოა გახსოვდეთ, რომ განტოლების ფესვები cos X = 0 მოცემულია ფორმულით

X = π / 2 +n π ; (5)

განტოლების ფესვები cos X = -1 მოცემულია ფორმულით

X = π + 2 მ π ; (6)

და ბოლოს, განტოლების ფესვები cos X = 1 მოცემულია ფორმულით

X = 2 მ π ; (7)

დასასრულს აღვნიშნავთ, რომ ფორმულები (4) , (5), (6) და (7) სწორია მხოლოდ იმ ვარაუდით, რომ სასურველი კუთხე X გამოხატულია რადიანებში. თუ ის გამოხატულია გრადუსით, მაშინ ეს ფორმულები ბუნებრივად უნდა შეიცვალოს. ასე რომ, ფორმულა (4) უნდა შეიცვალოს ფორმულით

X = ± რკალი ა+ 360° n,

ფორმულა (5) ფორმულა

X = 90° + 180° nდა ა.შ.