Tele2, 관세, 질문에 대한 도움말

자카로바 류드밀라 블라디미로브나
바르나울의 MBOU "중등학교 No. 59"
수학 선생님 [이메일 보호됨]

№1 가장 간단한 삼각 방정식

표적: 1. 다음 형식의 가장 간단한 삼각 방정식의 해에 대한 공식을 도출합니다. sinx=a, cosx=a, tgx=a, ctgx=a;

2. 공식을 사용하여 간단한 삼각 방정식을 푸는 방법을 배웁니다.

장비: 1) 삼각함수 그래프가 포함된 표 y= sinx, y=cosx, y=tgx, y=ctgx; 2) 역삼각 함수 값 표; 3) 간단한 삼각 방정식을 풀기 위한 공식 요약표입니다.

강의 수업 계획:

1 .방정식의 근에 대한 공식 유도

a) sinx =a,

b) cosx= ㅏ,

다) tgx= ㅏ,

d) ctgx= ㅏ.

2 . 받은 공식을 통합하기 위한 구강 정면 작업.

3 . 연구한 자료를 통합하기 위한 서면 작업

수업 중.

대수학, 기하학, 물리학 및 기타 과목에서 우리는 방정식 풀이를 포함한 다양한 문제에 직면합니다. 우리는 삼각 함수의 성질을 연구했으므로 함수 부호 아래에 미지수가 포함되어 있는 방정식으로 전환하는 것이 당연합니다.

정의: 형태의 방정식 죄악 = ㅏ , 코스엑스= ㅏ , tgx= ㅏ , ctgx= ㅏ 가장 간단한 삼각방정식이라고 합니다.

삼각 방정식을 푸는 모든 방법과 기술은 방정식을 가장 간단한 방정식으로 줄이는 것으로 구성되므로 가장 간단한 삼각 방정식을 푸는 방법을 배우는 것이 매우 중요합니다.

삼각 방정식을 풀 때 "적극적으로" 작동하는 공식을 유도하는 것부터 시작해 보겠습니다.

1. sinx 형식의 방정식 = ㅏ.

방정식 sinx =를 풀어 봅시다 ㅏ그래픽적으로. 이를 위해 하나의 좌표계에서 y=sinx 및 y= 함수의 그래프를 구성합니다. ㅏ.

1) 만일 ㅏ> 1 및 ㅏ죄 x= ㅏ직선과 사인파는 공통점이 없기 때문에 해가 없습니다.

2) -1a a가 사인파를 무한히 여러 번 교차하는 경우. 이는 방정식이죄x= ㅏ무한히 많은 솔루션을 가지고 있습니다.

사인주기는 2이므로 , 방정식을 풀기 위해죄x= ㅏ길이가 2인 임의의 세그먼트에서 모든 해를 찾는 것으로 충분합니다.

[-/2; /2] 아크사인의 정의에 따라 x=아크신 ㅏ, 그리고 x=-arcsin에서 ㅏ. 함수 у=sinx의 주기성을 고려하여 다음 표현식을 얻습니다.

x = -아크신 ㅏ+2n, nZ.

두 가지 솔루션 시리즈를 결합할 수 있습니다.

X = (-1) n 아크사인 ㅏ+n, nZ.

다음 세 가지 경우에는 일반적인 공식보다 간단한 관계를 사용하는 것을 선호합니다.

만약에 ㅏ=-1, 그러면 sin x =-1, x=-/2+2n

만약에 ㅏ=1이면 sin x =1, x =/2+2n

만약에 에이= 0이면 sin x =0입니다. x = n,

예: 방정식 풀기 sinx=1/2.

솔루션에 대한 공식을 만들어 봅시다 x=아크사인 1/2+ 2n

X= - 아크사인 a+2n

값을 계산해보자 arcsin1/2. 찾은 값을 해 공식에 대입해 보겠습니다.

x=5/6+2n

또는 일반 공식에 따라

X= (-1) n 아크사인 1/2+n,

X= (-1) n /6+n,

2. 형태의 방정식 cosx= ㅏ.

cosx= 방정식을 풀어봅시다. ㅏ또한 함수 y= cosx 및 y=를 도표화하여 그래픽적으로도 표시합니다. ㅏ.

1) 1이면 방정식은 다음과 같습니다. cosx= ㅏ그래프에 공통점이 없기 때문에 해결책이 없습니다.

2) -1인 경우 ㅏ cosx= ㅏ무한한 수의 솔루션을 가지고 있습니다.

우리는 모든 해결책을 찾아낼 것입니다 cosx= ㅏ코사인의 주기가 2이므로 길이가 2인 간격으로

아크 코사인의 정의에 따르면 방정식의 해는 다음과 같습니다. x=아르코스 에이. 코사인 함수의 패리티를 고려하면 [-;0] 방정식의 해는 x=-arcos가 됩니다. ㅏ.

따라서 방정식을 풀면 cosx= ㅏ x= + 아르코스 ㅏ+ 2n,

세 가지 경우에는 일반 공식을 사용하지 않고 더 간단한 관계를 사용합니다.

만약에 ㅏ=-1, cosx =-1, x =-/2+2n

만약에 ㅏ=1이면 cosx =1, x = 2n,

a=0이면 cosx=0입니다. x =/2+n

예: 방정식 풀기왜냐하면 x =1/2,

솔루션에 대한 공식을 만들어 봅시다 x=아코스 1/2+ 2n

값을 계산해보자 arccos1/2.

찾은 값을 해 공식에 대입해 보겠습니다.

X= + /3+ 2n, nZ.

형태의 방정식 tgx= ㅏ.

접선의 주기가 동일하므로 방정식의 모든 해를 찾으려면 tgx= ㅏ, 길이에 상관없이 모든 해를 구하는 것으로 충분합니다. 아크탄젠트의 정의에 따라 (-/2; /2) 방정식의 해는 arctan입니다. ㅏ. 함수의 기간을 고려하여 방정식의 모든 해는 다음 형식으로 작성할 수 있습니다.

x= 아크탄 ㅏ+ n, nZ.

예:방정식을 풀어보세요황갈색 x = 3/3

x=를 푸는 공식을 만들어 봅시다.아크탄 3/3 +n, nZ.

아크탄젠트 값을 계산해 봅시다 arctan 3/3= /6, 그러면

X=/6+ n, nZ.

방정식을 풀기 위한 공식 유도 와 함께 tgx= ㅏ학생들에게 제공될 수 있습니다.

예.

방정식을 풀어보세요 CTG x = 1.

x = 호сtg 1 + n, nZ,

X = /4 + n, nZ.

학습한 자료의 결과로 학생들은 다음 표를 작성할 수 있습니다.

"삼각 방정식 풀기."

방정식

연구된 자료를 통합하기 위한 연습입니다.

(구두) 공식을 사용하여 풀 수 있는 방정식은 무엇입니까?

a) x= (-1) n 아크사인 ㅏ+n, nZ;

b) x= + 아르코스 에이+ 2n?

cos x = 2/2, tan x= 1, sin x = 1/3, cos x = 3/3, sin x = -1/2, cos x= 2/3, sin x = 3, cos x = 2 .

다음 방정식 중 해가 없는 방정식은 무엇입니까?

방정식을 푼다:

a) 죄 x = 0; e) 죄 x = 2/2; h) 죄 x = 2;

b) cos x = 2/2; e) cos x = -1/2; i) cos x = 1;

d) tan x = 3; g) 침대 x = -1; j) 탄 x = 1/3.

3. 방정식을 푼다:

a) 죄 3x = 0; e) 2cos x = 1;

b) cos x/2 =1/2; e) 3tg 3x =1;

d) 죄 x/4 = 1; g) 2cos(2x+ /5) = 3.

이러한 방정식을 풀 때 다음 형식의 방정식을 푸는 규칙을 적어 두는 것이 유용합니다.죄 V x = ㅏ, 그리고 와 함께죄 V x = ㅏ, | ㅏ|1.

죄 V x = 에, |에|1.

V x = (-1) n 아크사인 ㅏ+n, nZ,

x= (-1) n 1/ V아크신 ㅏ+n/ V, 뉴질랜드.

수업 요약:

오늘 수업 시간에 우리는 간단한 삼각 방정식을 푸는 공식을 도출했습니다.

간단한 삼각 방정식을 푸는 예를 살펴보았습니다.

우리는 방정식을 푸는 데 사용할 표를 작성했습니다.

숙제.

№2 삼각 방정식 풀기

표적: 삼각 방정식을 풀기 위한 연구 방법: 1) 2차 방정식으로 축소 가능, 2) 동차 삼각 방정식으로 축소 가능.

삼각 방정식을 푸는 다양한 방법을 사용할 때 학생들의 관찰력을 개발합니다.

학생들과의 정면 작업.

삼각 방정식의 근에 대한 공식은 무엇입니까?왜냐하면 x= ㅏ, 죄 x= ㅏ, tgx = ㅏ, CTG x = ㅏ.

방정식을 푼다(구두로):

cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1.5, sin x=0.

오류를 찾아 오류의 원인을 생각해 보세요.

왜냐하면 x=1/2, x= + /6+2k,k 지.

사인 x= 3/2, x= /3+k, kZ.

tgx = /4, x=1+ k, kZ.

2. 새로운 자료를 연구합니다.

이 단원에서는 삼각 방정식을 푸는 가장 일반적인 방법 중 일부를 다룹니다.

삼각 방정식이 이차 방정식으로 축소되었습니다.

이 클래스에는 하나의 함수(사인 또는 코사인) 또는 동일한 인수의 두 함수를 포함하는 방정식이 포함될 수 있지만 그 중 하나는 기본 삼각법 항등식을 사용하여 두 번째 함수로 축소됩니다.

예를 들어, cosх가 짝수 거듭제곱으로 방정식을 입력하면 이를 1-sin 2 x로 바꾸고, sin 2 x인 경우 1-cos 2 x로 바꿉니다.

예.

방정식 풀기: 8죄 2 x - 6sin x -5 =0.

해결책: 다음을 나타내자 sin x=t, 그러면 8t 2 - 6t – 5=0,

D= 196,

T 1 = -1/2, t 2 = -5/4.

역대입을 수행하고 다음 방정식을 풀어보겠습니다.

X=(-1) k+1 /6+ k, kZ.

-5/4>1이므로 방정식에는 근이 없습니다.

답: x=(-1) k+1 /6+ k, kZ.

통합 운동 해결.

방정식을 푼다:

1) 2sin 2 x+ 3cos x = 0;

2) 5sin 2 x+ 6cos x -6 = 0;

3) 2sin 2 x+ 3cos 2 x = -2sin x;

4) 3tg2x+2tgx-1=0.

동차 삼각 방정식.

정의: 1) 형태의 방정식ㅏ 죄악 + 비 코스엑스=0, (a=0, b=0)를 sin x와 cos x에 대한 1차 동차방정식이라고 합니다.

이 방정식은 양변을 다음과 같이 나누어서 풀립니다.코스엑스 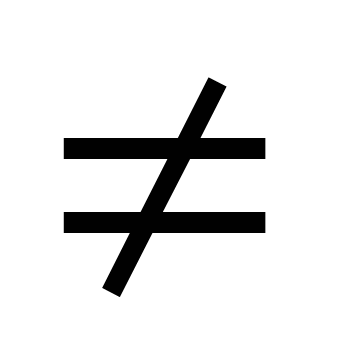0. 결과는 방정식이다 atgx+b=0.

2) 형태의 방정식ㅏ 죄 2 엑스 + 비 죄악 코스엑스 + 씨 코사인 2 엑스 =0 a, b, c는 임의의 숫자인 2차 동차 방정식이라고 합니다.

a = 0이면 양변을 다음으로 나누어 방정식을 푼다.왜냐하면 2x 0. 결과적으로 우리는 방정식을 얻습니다. atg 2 x+ btgx+с =0.

논평:형태의 방정식ㅏ 죄 mx + 비 코사인 mx=0 또는

ㅏ 죄 2 mx + 비 죄 mx 코사인 mx + 씨 코사인 2 mx =0 또한 균질합니다. 이를 해결하기 위해 방정식의 양쪽을 cos로 나눕니다. mx=0 아니면 코스 2 mx=0

3) 원래 동차방정식이 아닌 다양한 방정식이 동차방정식으로 환원될 수 있다. 예를 들어,죄 2 mx + 비 죄 mx 코사인 mx + 씨 코사인 2 mx = 디, 그리고 ㅏ 죄악 + 비 코스엑스= 디. 이 방정식을 풀려면 우변에 다음을 곱해야 합니다. "삼각 단위"저것들. ~에 죄 2 엑스 + 코사인 2 엑스수학적 변환을 수행합니다.

배운 자료를 통합하기 위한 연습:

1) 2sin x- 3cos x = 0; 5) 4죄 2x – 죄2x =3;

2) 죄 2x+ cos2x = 0; 6) 3sin 2 x + sinx cosx =2 cos 2 x ;

3) 죄 x+ 3cos x = 0; 7) 3 죄 2 x- 죄x cosx =2;

4) 사인 2 x -3 사인x cosx +2 cos 2 x =0

3. 수업을 요약합니다. 숙제.

이 수업에서는 그룹의 준비 상태에 따라 다음 형식의 방정식을 푸는 것을 고려할 수 있습니다. a sin mx +b cos mx=c, 여기서 a, b, c는 동시에 0이 아닙니다.

강화 운동:

1. 3sin x + cos x=2;

2. 3sin 2x + cos 2x= 2;

3. 사인 x/3 + cos x/3=1;

4. 12사인 x +5 cos x+13=0.

№ 3 삼각 방정식 풀기

표적: 1) 인수분해를 통해 삼각 방정식을 푸는 방법을 연구합니다. 다양한 삼각법 공식을 사용하여 삼각 방정식을 푸는 방법을 배웁니다.

2) 확인: 간단한 삼각 방정식을 푸는 공식에 대한 학생들의 지식; 간단한 삼각 방정식을 푸는 능력.

강의 계획:

숙제를 확인 중입니다.

수학적 받아쓰기.

새로운 자료를 학습합니다.

독립적 인 일.

수업을 요약합니다. 숙제.

수업 진행:

숙제 확인 중 (삼각 방정식의 해는 칠판에 간략하게 적혀 있습니다.)

수학적 받아쓰기.

1에

1. 가장 간단한 삼각 방정식이라고 불리는 방정식은 무엇입니까?

2. 형태의 방정식의 이름은 무엇입니까ㅏ 죄x + 비 cosx=0? 해결 방법을 알려주세요.

3.방정식의 근을 구하는 공식을 적으세요 tgx = ㅏ(ctg x= ㅏ).

4. 다음 형식의 방정식의 근에 대한 공식을 적습니다. cosx= ㅏ, 어디 ㅏ=1, ㅏ=0, ㅏ=-1.

5. 방정식의 근에 대한 일반 공식을 적어보세요죄 x= ㅏ, | ㅏ|

6. 형태의 방정식을 푸는 방법ㅏ cosx= 비, | 비|

2시에

1. 방정식의 근에 대한 공식을 적으세요 cosx= ㅏ,| ㅏ|

2. 방정식의 근에 대한 일반 공식을 적어보세요

= ㅏ, | ㅏ|

3. 형태의 방정식은 무엇입니까?죄 x= ㅏ, tgx = ㅏ, 죄 x= ㅏ?

4. 방정식의 근에 대한 공식을 적어보세요죄 x= ㅏ, 만약에 ㅏ=1, ㅏ=0, ㅏ=-1.

5. 형태의 방정식을 푸는 방법죄 ㅏ x= 비, | 비|

6. 2차 균질 방정식이라고 불리는 방정식은 무엇입니까? 어떻게 해결되나요?

새로운 자료를 학습합니다.

인수분해 방법.

삼각 방정식을 푸는 데 가장 일반적으로 사용되는 방법 중 하나는 인수분해 방법입니다.

방정식 f(x) =0이 f 1 (x) f 2 (x) =0으로 표현될 수 있는 경우 문제는 두 방정식 f 1 (x) = 0, f 2 (x) = 0을 푸는 것으로 축소됩니다. .

(학생들과 함께 규칙을 기억하는 것이 유용합니다. 요소 중 하나 이상이 0이고 나머지 요소가 의미가 있는 경우 요소의 곱은 0과 같습니다.»)

다양한 복잡성의 방정식을 풀어 연구 자료를 통합합니다.

(죄 x-1/2)(죄 x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(자기)

3) 죄 2 x+ 죄 x cosx=0; 4) 죄 2 x- 죄 x =0;

5) 죄 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2가지 방법)

7) cosx+ cos3x=0; 8) 죄 3x= 죄 17x;

9) 죄 x+ 죄 2x+ 죄 3x=0; 10) cos3x cos5x

11) 죄 x cos5x = 죄 9x cos3x 죄 2x 죄 2x

12) 3 cosx 죄 x+ cos 2 x=0(self)

13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.

독립적 인 일.

옵션-1 옵션-2

1) 6 죄 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;

2) 죄 2x – cos2x=0; 2) 3 cos x/2 - 사인 x/2=0;

3) 5 죄 2 x+ 죄 x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5;

4) 죄x+sin5x=sin3x+sin7x; 4) 죄 x-죄 2x +죄 3x-죄 4x=0;

5) 죄x+cosx=1. 5) 죄x+cosx=2.

8. 수업을 요약합니다. 숙제.

수업 유형:학습 과제 설정.

수업 목표:

교육적인: 간단한 삼각 방정식을 푸는 방법에 대한 학생들의 지식을 체계화하고 원과 표 작업 기술을 통합합니다.

발달: 삼각방정식 풀이를 위한 다양한 기법을 활용하여 학생들의 창의적 지적 능력 형성을 위한 노력을 지속합니다.

교육적인: 집단 정신 활동, 상호 지원 및 자신과 다른 관점 수용 기술을 개발합니다.

수업 중에는

1. 성공 상황.

방정식을 푼다: cosx=1; cosx=0; cosx= -1.

2. 지식과 무지 사이의 상황, 격차”.

방정식을 푼다: cosx=½; cosx=a.

논의.

3. 교육 과제에 대한 설명.

이 유형의 방정식을 푸는 방법은 무엇입니까?

1) 원점을 중심으로 점 (1;0)을 다음과 같은 각도만큼 회전시켜 얻은 단위원 위 점의 가로좌표는 무엇입니까?

2). 다음과 같습니다: ?

답변:

3).다음과 같습니다: .

답변:

;

;

(1) .

선생님의 말씀: 수학자들은 역코사인이라는 단어를 "아크코사인"이라는 단어라고 불렀습니다. 숫자의 아크코사인은 코사인이 a와 같은 숫자입니다.
arccosa=α, cosα=a이고 0≤α≤π인 경우.

4). arccos 기호를 사용하여 평등(1)을 씁니다.

5). 방정식을 푼다: cosx=½, cosx=α.

답: x=arccos½, x=arccosa.

6). 가로좌표가 ½인 단위원의 점 (1;0)의 회전 각도를 지정하십시오.

답: 점이 π/3 및 -π/3과 같은 각도로 회전할 때 가로좌표는 ½과 같습니다.

즉 x=±arccos½에서 cosx=½
x=±arccosa에서 cosx=a.

7). 점 (1;0)을 각도로 회전하여 얻은 점의 가로좌표는 무엇입니까: π/3+2π; π/3+6π; -π/3+4π; -π/3+8π; π/3+2πn; -π/3+2πn.

답: 가로좌표는 ½이고, x=±arccos½+2πn에서 cosx=½입니다.
x=±arccosa+2πn에서 cosx=a.

8). 결론: 방정식 cosx=a

1) ≤1이면 근이 있고,
2) >1이면 뿌리가 없습니다.

9). 강의 요약:

a) a와 α의 어떤 값에 대해 arccosa = α 등식이 의미가 있습니까?
b) a의 아크코사인은 무엇입니까?
c) 방정식 cosx=a는 a의 어떤 값에 근을 가집니까?
d) 방정식 cosx=a의 근을 구하는 공식.

가장 간단한 삼각 방정식은 다음 방정식입니다.

Cos(x) = a, sin(x) = a, tg(x) = a, ctg(x) =a

방정식 cos(x) = a

설명 및 근거

1. 방정식 cosx = a의 근입니다. 언제 | | > 1 방정식에는 근이 없습니다. 왜냐하면 | 코스엑스 |< 1 для любого x (прямая y = а при а >1 또는< -1 не пересекает график функцииy = cosx).

하자 | |< 1. Тогда прямая у = а пересекает график функции

y = cos x. 구간에서 함수 y = cos x는 1에서 -1로 감소합니다. 그러나 감소 함수는 정의 영역의 한 지점에서만 각 값을 취하므로 방정식 cos x = a는 이 구간에서 단 하나의 근을 가지며, 이는 아크코사인 정의에 따라 다음과 같습니다. x 1 = arccos a(그리고 이 루트의 경우 cos x = A)입니다.

코사인은 짝수 함수이므로 [-n; 0] 방정식 cos x = 또한 단 하나의 근(x 1 반대편 숫자)만 갖습니다.

x 2 = -arccos

따라서 간격 [-n; p] (길이 2p) 방정식 cos x = a | |< 1 имеет только корни x = ±arccos а.

함수 y = cos x는 주기가 2n인 주기이므로 다른 모든 근은 2n(n € Z)에서 찾은 근과 다릅니다. 방정식 cos x = a의 근에 대해 다음 공식을 얻습니다.

x = ±arccos a + 2pp, n £ Z.

1. 방정식 cosx = a를 푸는 특별한 경우.

다음과 같은 경우 방정식 cos x = a의 근에 대한 특별한 표기법을 기억해 두는 것이 유용합니다.

a = 0, a = -1, a = 1이며, 이는 단위원을 기준으로 하면 쉽게 구할 수 있습니다.

코사인은 단위원의 대응점의 가로좌표와 동일하므로 단위원의 대응점이 점 A 또는 점 B인 경우에만 cos x = 0을 얻습니다.

마찬가지로, cos x = 1은 단위원의 해당 점이 점 C인 경우에만 가능하므로,

x = 2πп, k € Z.

또한 cos x = -1인 경우와 단위원의 해당 점이 D인 경우에만, 따라서 x = n + 2n입니다.

방정식 sin(x) = a

설명 및 근거

1. 방정식 sinx = a의 근입니다. 언제 | | > 1 방정식에는 근이 없습니다. 왜냐하면 | 죄악 |< 1 для любого x (прямая y = а на рисунке при а >1 또는< -1 не пересекает график функции y = sinx).

예:

\(2\sin(⁡x) = \sqrt(3)\)
tg\((3x)=-\) \(\frac(1)(\sqrt(3))\)
\(4\cos^2⁡x+4\sin⁡x-1=0\)
\(\cos⁡4x+3\cos⁡2x=1\)

삼각 방정식을 푸는 방법:

모든 삼각 방정식은 다음 유형 중 하나로 축소되어야 합니다.

\(\sin⁡t=a\), \(\cos⁡t=a\), tg\(t=a\), ctg\(t=a\)

여기서 \(t\)는 x가 포함된 표현식이고, \(a\)는 숫자입니다. 이러한 삼각 방정식을 다음과 같이 부릅니다. 가장 단순한. () 또는 특수 공식을 사용하여 쉽게 풀 수 있습니다.

여기에서 간단한 삼각 방정식을 푸는 방법에 대한 인포그래픽을 참조하세요.

예 . 삼각 방정식 \(\sin⁡x=-\)\(\frac(1)(2)\)을 푼다.
해결책:

답변: \(\left[ \begin(gathered)x=-\frac(π)(6)+2πk, \\ x=-\frac(5π)(6)+2πn, \end(gathered)\right.\) \(k,n∈Z\)

삼각 방정식의 근에 대한 공식에서 각 기호의 의미를 참조하세요.

주목!\(\sin⁡x=a\) 및 \(\cos⁡x=a\) 방정식은 \(a ϵ (-무한대;-1)∪(1;무한)\)인 경우 해가 없습니다. 임의의 x에 대한 사인과 코사인은 \(-1\)보다 크거나 같고 \(1\)보다 작거나 같기 때문입니다.

\(-1<\sin x<1\) \(-1<\cos⁡x<<1\)

예 . 방정식 \(\cos⁡x=-1,1\)을 풉니다.
해결책: \(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
답변 : 해결책이 없습니다.

예 . 삼각 방정식 tg\(⁡x=1\)을 풉니다.
해결책:

숫자원을 이용하여 방정식을 풀어봅시다. 이를 위해: 1) 원을 만든다) 2) \(x\) 및 \(y\) 축과 접선 축(\(y\) 축에 평행한 점 \((0;1)\)을 통과함)을 구성합니다. 3) 접선축에 점 \(1\)을 표시합니다. 4) 이 점과 좌표의 원점인 직선을 연결합니다. 5) 이 선과 숫자원의 교차점을 표시하세요. 6) 다음 점의 값에 서명해 보겠습니다. \(\frac(π)(4)\) ,\(\frac(5π)(4)\) 7) 이 포인트의 값을 모두 적어보세요. 서로 정확히 \(π\) 거리에 위치하므로 모든 값을 하나의 공식으로 쓸 수 있습니다.

답변: \(x=\)\(\frac(π)(4)\) \(+πk\), \(k∈Z\).

예 . 삼각 방정식 \(\cos⁡(3x+\frac(π)(4))=0\)을 풉니다.
해결책:

다시 숫자원을 사용해 봅시다. 1) 원, 축 \(x\) 및 \(y\)를 구성합니다. 2) 코사인축(\(x\)축)에 \(0\)을 표시합니다. 3) 이 점을 통해 코사인 축에 수직인 선을 그립니다. 4) 수직선과 원의 교차점을 표시합니다. 5) 다음 포인트의 값에 서명합시다: \(-\) \(\frac(π)(2)\),\(\frac(π)(2)\). 6) 우리는 이 포인트의 전체 값을 기록하고 이를 코사인(코사인 내부에 있는 것)과 동일시합니다. \(3x+\)\(\frac(π)(4)\) \(=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\) \(3x+\)\(\frac(π)(4)\) \(=\)\(\frac(π)(2)\) \(+2πk\) \(3x+\)\(\frac( π)(4)\) \(=-\)\(\frac(π)(2)\) \(+2πk\) 8) 평소와 같이 \(x\)를 방정식으로 표현하겠습니다. 숫자를 \(π\)뿐만 아니라 \(1\), \(2\), \(\frac(1)(4)\) 등으로 처리하는 것을 잊지 마십시오. 이것은 다른 모든 숫자와 동일한 숫자입니다. 숫자 차별 금지! \(3x=-\)\(\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=-\)\ (\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=\)\(\frac(π)(4)\) \(+2πk\) \(|:3\) \(3x=-\)\(\frac(3π)(4)\) \(+2πk\) \(|:3\) \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\)

답변: \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\) , \(k∈Z\).

삼각 방정식을 가장 간단한 것으로 줄이는 것은 창의적인 작업입니다. 여기서는 방정식을 풀기 위해 두 가지 방법과 특별한 방법을 모두 사용해야 합니다.
- 방법 (통합 국가 시험에서 가장 인기 있음).
- 방법.
- 보조인수 방법.

이차 삼각 방정식을 푸는 예를 생각해 봅시다.

예 . 삼각 방정식 \(2\cos^2⁡x-5\cos⁡x+2=0\) 풀기
해결책:

\(2\cos^2⁡x-5\cos⁡x+2=0\)	\(t=\cos⁡x\)를 교체해 보겠습니다.
	우리의 방정식은 전형적이 되었습니다. 를 이용하여 해결할 수 있습니다.
\(D=25-4 \cdot 2 \cdot 2=25-16=9\)
\(t_1=\)\(\frac(5-3)(4)\) \(=\)\(\frac(1)(2)\) ; \(t_2=\)\(\frac(5+3)(4)\) \(=2\)	우리는 역 교체를합니다.
\(\cos⁡x=\)\(\frac(1)(2)\); \(\cos⁡x=2\)	숫자원을 사용하여 첫 번째 방정식을 푼다. 두 번째 방정식에는 해가 없습니다. 왜냐하면 \(\cos⁡x∈[-1;1]\)이며 모든 x에 대해 2와 같을 수 없습니다.
	이 지점에 있는 모든 숫자를 적어 봅시다.

답변: \(x=±\)\(\frac(π)(3)\) \(+2πk\), \(k∈Z\).

ODZ 연구를 통해 삼각 방정식을 푸는 예:

예시(사용) . 삼각 방정식 \(=0\) 풀기

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	분수가 있고 코탄젠트가 있습니다. 이는 우리가 그것을 적어야 함을 의미합니다. 코탄젠트는 실제로 분수라는 점을 상기시켜 드리겠습니다. ctg\(x=\)\(\frac(\cos⁡x)(\sin⁡x)\) 따라서 ctg\(x\)에 대한 ODZ: \(\sin⁡x≠0\).
ODZ: ctg\(x ≠0\); \(\sin⁡x≠0\) \(x≠±\)\(\frac(π)(2)\) \(+2πk\); \(x≠πn\); \(k,n∈Z\)	숫자원에 "해결되지 않은 부분"을 표시해 보겠습니다.
\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	ctg\(x\)를 곱하여 방정식의 분모를 제거해 보겠습니다. 위에서 ctg\(x ≠0\)라고 썼기 때문에 이렇게 할 수 있습니다.
\(2\cos^2⁡x-\sin⁡(2x)=0\)	사인에 대한 이중각 공식을 적용해 보겠습니다: \(\sin⁡(2x)=2\sin⁡x\cos⁡x\).
\(2\cos^2⁡x-2\sin⁡x\cos⁡x=0\)	코사인으로 나누기 위해 손을 뻗으면 뒤로 당겨보세요! 확실히 0이 아닌 경우 변수가 있는 표현식으로 나눌 수 있습니다(예: \(x^2+1.5^x\)). 대신 괄호 안에 \(\cos⁡x\)를 넣자.
\(\cos⁡x (2\cos⁡x-2\sin⁡x)=0\)	방정식을 두 개로 "분할"해 보겠습니다.
\(\cos⁡x=0\); \(2\cos⁡x-2\sin⁡x=0\)	숫자원을 이용하여 첫 번째 방정식을 풀어보겠습니다. 두 번째 방정식을 \(2\)로 나누고 \(\sin⁡x\)를 오른쪽으로 이동합니다.
\(x=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\). \(\cos⁡x=\sin⁡x\)	결과 루트는 ODZ에 포함되지 않습니다. 따라서 우리는 이에 대한 응답을 기록하지 않을 것입니다. 두 번째 방정식이 일반적입니다. \(\sin⁡x\)로 나누자(\(\sin⁡x=0\)는 방정식의 해가 될 수 없습니다. 이 경우 \(\cos⁡x=1\) 또는 \(\cos⁡ x=-1\)).
	우리는 다시 원을 사용합니다.
\(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\)	이러한 어근은 ODZ에서 제외되지 않으므로 답변에 적어주시면 됩니다.

답변: \(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\).

왜냐하면 방정식 엑스 = ㅏ

방정식의 각 근

코사인 엑스 = ㅏ (1)

정현파의 일부 교차점의 가로좌표로 간주될 수 있습니다. y = 왜냐하면엑스 직선으로 와이 =ㅏ , 그리고 반대로 각 교차점의 가로좌표는 방정식 (1)의 근 중 하나입니다. 따라서 방정식 (1)의 모든 근의 집합은 코사인 파동의 모든 교차점의 가로좌표 집합과 일치합니다. y = 왜냐하면엑스 직선으로 와이 = ㅏ .

만약에 | ㅏ| >1 , 그 다음은 코사인 y = 왜냐하면엑스 선과 교차하지 않음 와이 = ㅏ .

이 경우 방정식 (1)에는 근이 없습니다.

~에 |ㅏ| < 1 교차점이 무한히 많습니다.

> 0의 경우

한 동안< 0.

이러한 모든 교차점을 두 그룹으로 나눕니다.

A-2, A-1, A1, A2, ...,

B-2, B-1, B1, B2, ...,

점 ㅏ가로좌표가 있다 아르코스 ㅏ , 첫 번째 그룹의 다른 모든 점은 2의 배수인 거리에서 분리됩니다. π

아르코스 ㅏ+ 2천 π . (2)

점 안에, 그림에서 쉽게 이해할 수 있듯이 가로좌표가 있습니다. - 아르코스ㅏ , 두 번째 그룹의 다른 모든 점은 2의 배수인 거리에서 제거됩니다. π . 따라서 가로좌표는 다음과 같이 표현됩니다.

아르코스 ㅏ+ 2nπ . (3)

따라서 식 (1)에는 식 (2)와 (3)에 의해 정의된 두 개의 근 그룹이 있습니다. 하지만 이 두 공식은 분명히 하나의 공식으로 쓸 수 있습니다.

엑스 = ± 아크코스 ㅏ+ 2m π , (4)

어디 중모든 정수(m = 0, ±1, ±2, ±3, ...)를 통과합니다.

이 공식을 도출할 때 수행한 추론은 다음과 같은 경우에만 정확합니다.
| ㅏ| =/= 1. 그러나 형식적으로는 관계 (4) 방정식의 모든 근을 결정합니다. 코사인x=a 그리고 | ㅏ| =1. (증명해 보세요!) 그러므로 우리는 공식을 다음과 같이 말할 수 있습니다. (4) 모든 값에 대해 방정식 (1)의 모든 근을 제공합니다. ㅏ , 만약에 |ㅏ| < 1 .

그러나 여전히 세 가지 특별한 경우( ㅏ = 0, ㅏ = -1, ㅏ= +1) 공식을 사용하지 않는 것이 좋습니다. (4) , 그러나 다른 관계를 사용하십시오. 방정식의 근이 다음과 같다는 것을 기억하는 것이 유용합니다. 코사인 엑스 = 0 공식에 의해 주어진다

엑스 = π / 2 +n π ; (5)

방정식의 근 코사인 엑스 = -1 공식에 의해 주어진다

엑스 = π + 2m π ; (6)

그리고 마지막으로 방정식의 근본 코사인 엑스 = 1 공식에 의해 주어진다

엑스 = 2m π ; (7)

결론적으로 우리는 공식에 주목합니다. (4) , (5), (6) 및 (7)은 원하는 각도가 엑스 라디안으로 표현됩니다. 각도로 표현한다면 공식을 자연스럽게 바꿔야 합니다. 그래서, 공식은 (4) 공식으로 대체해야합니다

엑스 = ± 아크코스 ㅏ+ 360° n,

공식 (5) 공식

엑스 = 90° + 180°n등.