Pomoć na Tele2, tarife, pitanja

Zakharova Lyudmila Vladimirovna
MBOU "Srednja škola br. 59" u Barnaulu
profesorica matematike [e-mail zaštićen]

№1 Najjednostavnije trigonometrijske jednadžbe

Cilj: 1. Izvesti formule za rješenja najjednostavnijih trigonometrijskih jednadžbi oblika sinx =a, cosx=a, tgx=a, ctgx=a;

2. Naučiti rješavati jednostavne trigonometrijske jednadžbe pomoću formula.

Oprema: 1) Tablice s grafovima trigonometrijskih funkcija y= sinx, y=cosx, y=tgx, y=ctgx; 2) Tablica vrijednosti inverznih trigonometrijskih funkcija; 3) Zbirna tablica formula za rješavanje jednostavnih trigonometrijskih jednadžbi.

Plan predavanja:

1 .Izvođenje formula za korijene jednadžbe

a) sinx =a,

b) cosx= a,

c) tgx= a,

d) ctgx= A.

2 . Usmeni frontalni rad na učvršćivanju dobivenih formula.

3 . Pisani rad za konsolidaciju proučenog gradiva

Tijekom nastave.

U algebri, geometriji, fizici i drugim predmetima susrećemo se s raznim problemima čije rješavanje uključuje rješavanje jednadžbi. Proučavali smo svojstva trigonometrijskih funkcija, pa je prirodno obratiti se na jednadžbe u kojima je nepoznanica sadržana pod predznakom funkcije

Definicija: Jednadžbe oblika sinx = a , cosx= a , tgx= a , ctgx= A nazivaju se najjednostavnije trigonometrijske jednadžbe.

Vrlo je važno naučiti rješavati najjednostavnije trigonometrijske jednadžbe, budući da se sve metode i tehnike rješavanja bilo koje trigonometrijske jednadžbe sastoje u njihovom reduciranju na najjednostavnije.

Počnimo s izvođenjem formula koje “aktivno” rade pri rješavanju trigonometrijskih jednadžbi.

1.Jednadžbe oblika sinx = a.

Riješimo jednadžbu sinx = a grafički. Da bismo to učinili, u jednom koordinatnom sustavu ćemo konstruirati grafove funkcija y=sinx i y= A.

1) Ako A> 1 i A grijeh x= A nema rješenja, budući da pravac i sinusni val nemaju zajedničkih točaka.

2) Ako -1a a prelazi sinusni val beskonačno mnogo puta. To znači da jednadžba sinx= a ima beskonačno mnogo rješenja.

Budući da je period sinusa 2 , zatim riješiti jednadžbu sinx= a dovoljno je pronaći sva rješenja na bilo kojem segmentu duljine 2.

Rješavanje jednadžbe na [-/2; /2] po definiciji arkusina x= arcsin a, a na x=-arcsin a. Uzimajući u obzir periodičnost funkcije u=sinx, dobivamo sljedeće izraze

x = -arcsin a+2n, n Z.

Obje serije rješenja mogu se kombinirati

X = (-1) n arcsin a+n, nZ.

U sljedeća tri slučaja radije koriste jednostavnije relacije nego opću formulu:

Ako A=-1, tada sin x =-1, x=-/2+2n

Ako A=1, tada sin x =1, x =/2+2n

Ako a= 0, tada je sin x =0. x = n,

Primjer: Riješite jednadžbu sinx =1/2.

Kreirajmo formule za rješenja x=arcsin 1/2+ 2n

X= - arcsin a+2n

Izračunajmo vrijednost arcsin1/2. Zamijenimo pronađenu vrijednost u formule rješenja

x=5/6+2n

ili prema općoj formuli

X= (-1) n arcsin 1/2+n,

X= (-1) n /6+n,

2. Jednadžbe oblika cosx= a.

Riješimo jednadžbu cosx= a također grafički, iscrtavanjem funkcija y= cosx i y= A.

1) Ako je 1, onda je jednadžba cosx= a nema rješenja jer grafovi nemaju zajedničkih točaka.

2) Ako je -1 a cosx= a ima beskonačan broj rješenja.

Naći ćemo sva rješenja cosx= a na intervalu duljine 2 jer je period kosinusa 2.

Prema definiciji ark kosinusa, rješenje jednadžbe bit će x= arcos a. S obzirom na paritet kosinusne funkcije, rješenje jednadžbe na [-;0] bit će x=-arcos a.

Dakle, rješavanje jednadžbe cosx= a x= + arcos a+ 2 n,

U tri slučaja nećemo koristiti opću formulu, već jednostavnije relacije:

Ako A=-1, tada cosx =-1, x =-/2+2n

Ako A=1, tada je cosx =1, x = 2n,

Ako je a=0, tada je cosx=0. x =/2+n

Primjer: Riješite jednadžbu cos x =1/2,

Kreirajmo formule za rješenja x=arccos 1/2+ 2n

Izračunajmo vrijednost arccos1/2.

Zamijenimo pronađenu vrijednost u formule rješenja

X= + /3+ 2n, nZ.

Jednadžbe oblika tgx= a.

Budući da je period tangente jednak, tada da bismo pronašli sva rješenja jednadžbe tgx= a, dovoljno je pronaći sva rješenja na bilo kojem intervalu duljine . Prema definiciji arktangensa, rješenje jednadžbe na (-/2; /2) je arktan a. Uzimajući u obzir period funkcije, sva rješenja jednadžbe mogu se napisati u obliku

x= arktan a+ n, nZ.

Primjer: Riješite jednadžbu tan x = 3/3

Kreirajmo formulu za rješavanje x= arktan 3/3 +n, nZ.

Izračunajmo vrijednost arktangensa arctan 3/3= /6, dakle

X=/6+ n, nZ.

Izvođenje formule za rješavanje jednadžbe S tgx= a mogu se pružiti studentima.

Primjer.

Riješite jednadžbu ctg x = 1.

x = arcctg 1 + n, nZ,

X = /4 + n, nZ.

Kao rezultat proučavanog materijala, studenti mogu ispuniti tablicu:

"Rješavanje trigonometrijskih jednadžbi."

jednadžba

Vježbe za učvršćivanje naučenog gradiva.

(usmeno) Koja se od napisanih jednadžbi može riješiti pomoću formula:

a) x= (-1) n arcsin a+n, nZ;

b) x= + arcos a+ 2n?

cos x = 2/2, tan x = 1, sin x = 1/3, cos x = 3/3, sin x = -1/2, cos x = 2/3, sin x = 3, cos x = 2 .

Koja od sljedećih jednadžbi nema rješenja?

Riješite jednadžbe:

a) sin x = 0; e) sin x = 2/2; h) sin x = 2;

b) cos x = 2/2; e) cos x = -1/2; i) cos x = 1;

d) tan x = 3; g) krevetić x = -1; j) tan x = 1/3.

3. Riješite jednadžbe:

a) sin 3x = 0; e) 2cos x = 1;

b) cos x/2 =1/2; e) 3 tg 3x =1;

d) sin x/4 = 1; g) 2cos(2x+ /5) = 3.

Pri rješavanju ovih jednadžbi korisno je zapisati pravila za rješavanje jednadžbi oblika grijeh V x = a, I S grijeh V x = a, | a|1.

Grijeh V x = a, |a|1.

V x = (-1) n arcsin a+n, nZ,

x= (-1) n 1/ V arcsin a+n/ V, nZ.

Sažimanje lekcije:

Danas smo na satu izvodili formule za rješavanje jednostavnih trigonometrijskih jednadžbi.

Pogledali smo primjere rješavanja jednostavnih trigonometrijskih jednadžbi.

Ispunili smo tablicu koju ćemo koristiti za rješavanje jednadžbi.

Domaća zadaća.

№2 Rješavanje trigonometrijskih jednadžbi

Cilj: Metode proučavanja rješavanja trigonometrijskih jednadžbi: 1) svodljive na kvadratne, 2) svodljive na homogene trigonometrijske jednadžbe.

Razvijati sposobnost zapažanja učenika pri korištenju različitih metoda rješavanja trigonometrijskih jednadžbi.

Frontalni rad s učenicima.

Koje su formule za korijene trigonometrijskih jednadžbi? cos x= a, sin x= a, tgx = a, ctg x = a.

Riješite jednadžbe (usmeno):

cos x=-1, sin x=0, tgx =0, cos x=1, cos x=1,5, sin x=0.

Pronađite pogreške i razmislite o razlozima za pogreške.

cos x=1/2, x= + /6+2k,k Z.

sin x= 3/2, x= /3+k, kZ.

tgx = /4, x=1+ k, kZ.

2. Učenje novog gradiva.

Ova lekcija će pokriti neke od najčešćih metoda za rješavanje trigonometrijskih jednadžbi.

Trigonometrijske jednadžbe svedene na kvadratne.

Ova klasa može uključivati ​​jednadžbe koje uključuju jednu funkciju (sinus ili kosinus) ili dvije funkcije istog argumenta, ali je jedna od njih reducirana na drugu pomoću osnovnih trigonometrijskih identiteta.

Na primjer, ako cosh ulazi u jednadžbu u parnim potencijama, tada ga zamijenimo s 1-sin 2 x, ako je sin 2 x, tada ga zamijenimo s 1-cos 2 x.

Primjer.

Riješite jednadžbu: 8 sin 2 x - 6sin x -5 =0.

Rješenje: Označimo sin x=t, tada je 8t 2 - 6t – 5=0,

D = 196,

T1 = -1/2, t2 = -5/4.

Izvršimo obrnutu zamjenu i riješimo sljedeće jednadžbe.

X=(-1) k+1 /6+ k, kZ.

Budući da je -5/4>1, jednadžba nema korijena.

Odgovor: x=(-1) k+1 /6+ k, kZ.

Rješavanje vježbi konsolidacije.

Riješite jednadžbu:

1) 2sin 2 x+ 3cos x = 0;

2) 5sin 2 x+ 6cos x -6 = 0;

3) 2sin 2 x+ 3cos 2 x = -2sin x;

4) 3 tg 2 x +2 tgx-1=0.

Homogene trigonometrijske jednadžbe.

Definicija: 1) Jednadžba oblikaa sinx + b cosx=0, (a=0, b=0) naziva se homogena jednadžba prvog stupnja s obzirom na sin x i cos x.

Ova se jednadžba rješava dijeljenjem obje strane s cosx 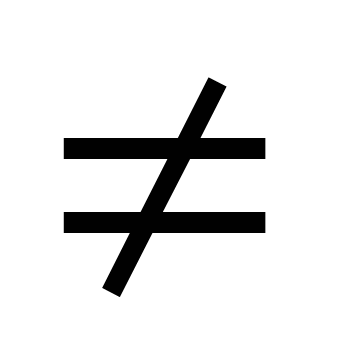0. Rezultat je jednadžba atgx+ b=0.

2) Jednadžba oblikaa grijeh 2 x + b sinx cosx + c cos 2 x =0 naziva se homogena jednadžba drugog stupnja, gdje su a, b, c bilo koji brojevi.

Ako je a = 0, tada jednadžbu rješavamo dijeljenjem obje strane s cos 2 x 0. Kao rezultat toga dobivamo jednadžbu atg 2 x+ btgx+s =0.

Komentar: Jednadžba oblikaa grijeh mx + b cos mx=0 ili

a grijeh 2 mx + b grijeh mx cos mx + c cos 2 mx =0 također su homogeni. Da bismo ih riješili, obje strane jednadžbe podijelimo s cos mx=0 ili cos 2 mx=0

3) Razne jednadžbe koje izvorno nisu homogene jednadžbe mogu se svesti na homogene jednadžbe. Na primjer,grijeh 2 mx + b grijeh mx cos mx + c cos 2 mx = d, I a sinx + b cosx= d. Da biste riješili ove jednadžbe, morate desnu stranu pomnožiti s "trigonometrijska jedinica" oni. na grijeh 2 x + cos 2 x i izvoditi matematičke transformacije.

Vježbe za konsolidaciju proučenog materijala:

1) 2sin x- 3cos x = 0; 5) 4 sin 2 x – sin2x =3;

2) sin 2x+ cos2x = 0; 6) 3 sin 2 x + sinx cosx =2 cos 2 x ;

3) sin x+ 3cos x = 0; 7) 3 sin 2 x- sinx cosx =2;

4) sin 2 x -3 sinx cosx +2 cos 2 x =0

3. Sažimanje lekcije. Domaća zadaća.

U ovoj lekciji, ovisno o pripremljenosti grupe, možete razmotriti rješavanje jednadžbi oblika a sin mx +b cos mx=c, gdje a, b, c nisu istovremeno jednaki nuli.

Vježbe jačanja:

1. 3sin x + cos x=2;

2. 3sin 2x + cos 2x= 2;

3. sin x/3 + cos x/3=1;

4. 12 sin x +5 cos x+13=0.

№ 3 Rješavanje trigonometrijskih jednadžbi

Cilj: 1) Proučiti metodu rješavanja trigonometrijskih jednadžbi faktorizacijom; naučiti rješavati trigonometrijske jednadžbe pomoću različitih trigonometrijskih formula;

2) Provjera: znanja učenika o formulama za rješavanje jednostavnih trigonometrijskih jednadžbi; sposobnost rješavanja jednostavnih trigonometrijskih jednadžbi.

Plan učenja:

Provjera domaće zadaće.

Matematički diktat.

Učenje novog gradiva.

Samostalni rad.

Sažimanje lekcije. Domaća zadaća.

Napredak lekcije:

Provjera domaće zadaće (rješenja trigonometrijskih jednadžbi ukratko su ispisana na ploči).

Matematički diktat.

U 1

1. Koje se jednadžbe nazivaju najjednostavnijim trigonometrijskim jednadžbama?

2. Kako se zove jednadžba oblikaa sinx + b cosx=0? Navedite način rješavanja.

3. Zapišite formulu za korijene jednadžbe tgx = a(ctg x= a).

4. Napiši formule za korijene jednadžbi oblika cosx= a, Gdje A=1, A=0, A=-1.

5. Zapišite opću formulu za korijene jednadžbe grijeh x= a, | a|

6. Kako se rješavaju jednadžbe oblikaa cosx= b, | b|

U 2

1. Napiši formule za korijene jednadžbi cosx= a,| a|

2. Zapišite opću formulu za korijene jednadžbe

= a, | a|

3. Kako se nazivaju jednadžbe oblika? grijeh x= a, tgx = a, grijeh x= a?

4. Zapišite formule za korijene jednadžbe grijeh x= a, Ako A=1, A=0, A=-1.

5. Kako se rješavaju jednadžbe oblika grijeh a x= b, | b|

6. Koje se jednadžbe nazivaju homogenim jednadžbama drugog stupnja? Kako se rješavaju?

Učenje novog gradiva.

Metoda faktorizacije.

Jedna od najčešće korištenih metoda za rješavanje trigonometrijskih jednadžbi je metoda faktorizacije.

Ako se jednadžba f(x) =0 može prikazati kao f 1 (x) f 2 (x) =0, tada se problem svodi na rješavanje dvije jednadžbe f 1 (x) = 0, f 2 (x) = 0 .

(S učenicima je korisno zapamtiti pravilo “ Umnožak faktora jednak je nuli ako je barem jedan od faktora jednak nuli, a ostali imaju smisla»)

Učvršćivanje naučenog gradiva kroz rješavanje jednadžbi različite složenosti.

(sin x-1/2)(sin x+1)=0; 2) (cosx- 2/2)(sin x+ 2/2)=0;(sam)

3) sin 2 x+ sin x cosx=0; 4) sin 2 x- sin x =0;

5) sin 2x – cosx=0; 6) 4 cos 2 x -1 =0; (2 načina)

7) cosx+ cos3x=0; 8) grijeh 3x= grijeh 17x;

9) sin x+ sin 2x+ sin 3x=0; 10) cos3x cos5x

11) sin x cos5x = sin 9x cos3x sin 2x sin 2x

12) 3 cosx sin x+ cos 2 x=0(sam)

13) 2 cos 2 x - sin (x- /2)+ tanx tan (x+/2)=0.

Samostalni rad.

Opcija-1 Opcija-2

1) 6 sin 2 x+ 5sin x -1=0; 1) 3 cos 2 x+2 cosx -5=0;

2) sin 2x – cos2x=0; 2) 3 cos x/2 - sin x/2=0;

3) 5 sin 2 x+ sin x cosx -2 cos 2 x=2; 3) 4sin 2 x- sin x cosx +7cos 2 x=5;

4) sin x+sin5x=sin3x+sin7x; 4) sin x-sin 2x +sin 3x-sin 4x=0;

5) sin x+cosx=1. 5) sin x+cosx=2.

8. Sažimanje lekcije. Domaća zadaća.

Vrsta lekcije: postavljanje zadatka učenja.

Ciljevi lekcije:

Edukativni: usustaviti znanja učenika o metodama rješavanja jednostavnih trigonometrijskih jednadžbi, učvrstiti vještine rada s kružnicama i tablicama.

Razvojni: nastaviti rad na formiranju kreativnih intelektualnih sposobnosti učenika korištenjem različitih tehnika rješavanja trigonometrijskih jednadžbi.

Edukativni: razvijati vještine kolektivne mentalne aktivnosti, međusobne podrške i prihvaćanja gledišta različitog od vlastitog.

Tijekom nastave

1. Situacija uspjeha.

Riješite jednadžbu: cosx=1; cosx=0; cosx= -1.

2. Situacija, jaz” između znanja i neznanja.

Riješite jednadžbu: cosx=½; cosx=a.

Rasprava.

3. Izjava obrazovnog zadatka.

Kako riješiti jednadžbu ovog tipa?

1) Kolika je apscisa točke na jediničnoj kružnici dobivenoj rotacijom točke (1;0) oko ishodišta za kut jednak: ?

2). Što je jednako: ?

Odgovor:

3).Što je jednako: .

Odgovor:

;

;

(1) .

Riječi učitelja: matematičari su riječi reverse cos nazvali riječju arkosinus (arccos). Arkus kosinus broja je broj čiji je kosinus jednak a:
arccosa=α,ako je cosα=a i 0≤α≤π.

4). Napiši jednakost (1) koristeći simbol arccos.

5). Riješite jednadžbe: cosx=½, cosx=α.

Odgovor: x=arccos½, x=arccosa.

6). Imenujte kutove rotacije točke (1;0) jedinične kružnice kojoj je apscisa jednaka ½.

Odgovor: apscisa je jednaka ½ kada se točka zakrene za kut jednak π/3 i -π/3.

tj. cosx=½ pri x=±arccos½
cosx=a pri x=±arccosa.

7). Kolike su apscise točaka dobivenih rotacijom točke (1;0) za kutove: π/3+2π; π/3+6π; -π/3+4π; -π/3+8π; π/3+2πn; -π/3+2πn.

Odgovor: apscisa je ½, a cosx=½ na x=±arccos½+2πn,.
cosx=a pri x=±arccosa+2πn,.

8). Zaključak: jednadžba cosx=a

1) ima korijene ako je ≤1,
2) nema korijena ako je >1.

9). Sažetak lekcije:

a) Za koje vrijednosti a i α ima smisla jednakost arccosa = α?
b) Što se naziva arc kosinus od a?
c) Pri kojim vrijednostima a jednadžba cosx=a ima korijene?
d) Formula za pronalaženje korijena jednadžbe cosx=a.

Najjednostavnije trigonometrijske jednadžbe su jednadžbe

Cos (x) = a, sin (x) = a, tg (x) = a, ctg (x) = a

Jednadžba cos(x) = a

Obrazloženje i obrazloženje

1. Korijeni jednadžbe cosx = a. Kada | a | > 1 jednadžba nema korijena, jer | cosx |< 1 для любого x (прямая y = а при а >1 ili na a< -1 не пересекает график функцииy = cosx).

Neka | a |< 1. Тогда прямая у = а пересекает график функции

y = cos x. Na intervalu funkcija y = cos x opada od 1 do -1. Ali opadajuća funkcija uzima svaku od svojih vrijednosti samo u jednoj točki svoje domene definicije, stoga jednadžba cos x = a ima samo jedan korijen na ovom intervalu, koji je, prema definiciji arkosinusa, jednak: x 1 = arccos a (i za ovaj korijen cos x = A).

Kosinus je parna funkcija, pa na intervalu [-n; 0] jednadžba cos x = i također ima samo jedan korijen - broj nasuprot x 1, tj

x 2 = -arccos a.

Dakle, na intervalu [-n; p] (duljina 2p) jednadžba cos x = a s | a |< 1 имеет только корни x = ±arccos а.

Funkcija y = cos x je periodična s periodom 2n, stoga se svi ostali korijeni razlikuju od onih koji se nalaze s 2n (n € Z). Dobivamo sljedeću formulu za korijene jednadžbe cos x = a kada

x = ±arccos a + 2pp, n £ Z.

1. Posebni slučajevi rješavanja jednadžbe cosx = a.

Korisno je zapamtiti posebne oznake za korijene jednadžbe cos x = a kada

a = 0, a = -1, a = 1, što se lako može dobiti korištenjem jedinične kružnice kao reference.

Budući da je kosinus jednak apscisi odgovarajuće točke jedinične kružnice, dobivamo da je cos x = 0 ako i samo ako je odgovarajuća točka jedinične kružnice točka A ili točka B.

Slično, cos x = 1 ako i samo ako je odgovarajuća točka jedinične kružnice točka C, dakle,

x = 2πp, k € Z.

Također cos x = -1 ako i samo ako je odgovarajuća točka jedinične kružnice točka D, dakle x = n + 2n,

Jednadžba sin(x) = a

Obrazloženje i obrazloženje

1. Korijeni jednadžbe sinx = a. Kada | a | > 1 jednadžba nema korijena, jer | sinx |< 1 для любого x (прямая y = а на рисунке при а >1 ili na a< -1 не пересекает график функции y = sinx).

Primjeri:

\(2\sin(⁡x) = \sqrt(3)\)
tg\((3x)=-\) \(\frac(1)(\sqrt(3))\)
\(4\cos^2⁡x+4\sin⁡x-1=0\)
\(\cos⁡4x+3\cos⁡2x=1\)

Kako riješiti trigonometrijske jednadžbe:

Svaku trigonometrijsku jednadžbu treba svesti na jednu od sljedećih vrsta:

\(\sin⁡t=a\), \(\cos⁡t=a\), tg\(t=a\), ctg\(t=a\)

gdje je \(t\) izraz s x, \(a\) je broj. Takve trigonometrijske jednadžbe nazivaju se najjednostavniji. Mogu se lako riješiti pomoću () ili posebnim formulama:

Infografike o rješavanju jednostavnih trigonometrijskih jednadžbi pogledajte ovdje:, i.

Primjer . Riješite trigonometrijsku jednadžbu \(\sin⁡x=-\)\(\frac(1)(2)\).
Riješenje:

Odgovor: \(\lijevo[ \begin(sakupljeno)x=-\frac(π)(6)+2πk, \\ x=-\frac(5π)(6)+2πn, \end(sakupljeno)\desno.\) \(k,n∈Z\)

Što svaki simbol znači u formuli za korijene trigonometrijskih jednadžbi, vidi.

Pažnja! Jednadžbe \(\sin⁡x=a\) i \(\cos⁡x=a\) nemaju rješenja ako \(a ϵ (-∞;-1)∪(1;∞)\). Budući da su sinus i kosinus za bilo koji x veći ili jednak \(-1\) i manji ili jednaki \(1\):

\(-1≤\sin x≤1\) \(-1≤\cos⁡x≤1\)

Primjer . Riješite jednadžbu \(\cos⁡x=-1,1\).
Riješenje: \(-1,1<-1\), а значение косинуса не может быть меньше \(-1\). Значит у уравнения нет решения.
Odgovor : nema rješenja.

Primjer . Riješite trigonometrijsku jednadžbu tg\(⁡x=1\).
Riješenje:

Riješimo jednadžbu pomoću brojčane kružnice. Za ovo: 1) Konstruirajte krug) 2) Konstruirajte osi \(x\) i \(y\) te os tangente (prolazi točkom \((0;1)\) paralelno s osi \(y\)). 3) Na osi tangente označite točku \(1\). 4) Spojite ovu točku i ishodište koordinata - ravnom crtom. 5) Označite sjecišta ovog pravca i brojevne kružnice. 6) Potpišimo vrijednosti ovih točaka: \(\frac(π)(4)\) ,\(\frac(5π)(4)\) 7) Zapišite sve vrijednosti ovih točaka. Budući da se nalaze na udaljenosti od točno \(π\) jedna od druge, sve vrijednosti mogu se napisati u jednoj formuli:

Odgovor: \(x=\)\(\frac(π)(4)\) \(+πk\), \(k∈Z\).

Primjer . Riješite trigonometrijsku jednadžbu \(\cos⁡(3x+\frac(π)(4))=0\).
Riješenje:

Upotrijebimo ponovno brojčani krug. 1) Konstruirajte kružnicu, osi \(x\) i \(y\). 2) Na kosinusnoj osi (\(x\) os), označite \(0\). 3) Kroz ovu točku povucite okomicu na kosinusnu os. 4) Označite sjecišta okomice i kružnice. 5) Potpišimo vrijednosti ovih točaka: \(-\) \(\frac(π)(2)\),\(\frac(π)(2)\). 6) Zapišemo cijelu vrijednost tih točaka i izjednačimo ih s kosinusom (s onim što je unutar kosinusa). \(3x+\)\(\frac(π)(4)\) \(=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\) \(3x+\)\(\frac(π)(4)\) \(=\)\(\frac(π)(2)\) \(+2πk\) \(3x+\)\(\frac( π)(4)\) \(=-\)\(\frac(π)(2)\) \(+2πk\) 8) Kao i obično, izrazit ćemo \(x\) u jednadžbama. Ne zaboravite tretirati brojeve s \(π\), kao i \(1\), \(2\), \(\frac(1)(4)\), itd. To su isti brojevi kao i svi ostali. Nema numeričke diskriminacije! \(3x=-\)\(\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=-\)\ (\frac(π)(4)\) \(+\)\(\frac(π)(2)\) \(+2πk\) \(3x=\)\(\frac(π)(4)\) \(+2πk\) \(|:3\) \(3x=-\)\(\frac(3π)(4)\) \(+2πk\) \(|:3\) \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\)

Odgovor: \(x=\)\(\frac(π)(12)\) \(+\)\(\frac(2πk)(3)\) \(x=-\)\(\frac(π)( 4)\) \(+\)\(\frac(2πk)(3)\) , \(k∈Z\).

Svođenje trigonometrijskih jednadžbi na najjednostavnije je kreativan zadatak, ovdje morate koristiti obje i posebne metode za rješavanje jednadžbi:
- Metoda (najpopularnija u Jedinstvenom državnom ispitu).
- Metoda.
- Metoda pomoćnih argumenata.

Razmotrimo primjer rješavanja kvadratne trigonometrijske jednadžbe

Primjer . Riješite trigonometrijsku jednadžbu \(2\cos^2⁡x-5\cos⁡x+2=0\)
Riješenje:

\(2\cos^2⁡x-5\cos⁡x+2=0\)	Izvršimo zamjenu \(t=\cos⁡x\).
	Naša je jednadžba postala tipična. Možete ga riješiti pomoću .
\(D=25-4 \cdot 2 \cdot 2=25-16=9\)
\(t_1=\)\(\frac(5-3)(4)\) \(=\)\(\frac(1)(2)\) ; \(t_2=\)\(\frac(5+3)(4)\) \(=2\)	Vršimo obrnutu zamjenu.
\(\cos⁡x=\)\(\frac(1)(2)\); \(\cos⁡x=2\)	Prvu jednadžbu rješavamo pomoću brojevnog kruga. Druga jednadžba nema rješenja jer \(\cos⁡x∈[-1;1]\) i ne može biti jednako dva za bilo koji x.
	Zapišimo sve brojeve koji leže u tim točkama.

Odgovor: \(x=±\)\(\frac(π)(3)\) \(+2πk\), \(k∈Z\).

Primjer rješavanja trigonometrijske jednadžbe s proučavanjem ODZ:

Primjer (USE) . Riješite trigonometrijsku jednadžbu \(=0\)

\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Postoji razlomak i postoji kotangens - to znači da ga trebamo zapisati. Dopustite mi da vas podsjetim da je kotangens zapravo razlomak: ctg\(x=\)\(\frac(\cos⁡x)(\sin⁡x)\) Prema tome, ODZ za ctg\(x\): \(\sin⁡x≠0\).
ODZ: ctg\(x ≠0\); \(\sin⁡x≠0\) \(x≠±\)\(\frac(π)(2)\) \(+2πk\); \(x≠πn\); \(k,n∈Z\)	Označimo “nerješenja” na brojevnoj kružnici.
\(\frac(2\cos^2⁡x-\sin(⁡2x))(ctg x)\)\(=0\)	Oslobodimo se nazivnika u jednadžbi množenjem sa ctg\(x\). To možemo učiniti jer smo gore napisali da je ctg\(x ≠0\).
\(2\cos^2⁡x-\sin⁡(2x)=0\)	Primijenimo formulu dvostrukog kuta za sinus: \(\sin⁡(2x)=2\sin⁡x\cos⁡x\).
\(2\cos^2⁡x-2\sin⁡x\cos⁡x=0\)	Ako ruke ispružite da dijelite s kosinusom, povucite ih natrag! Možete dijeliti izrazom s varijablom ako ona definitivno nije jednaka nuli (na primjer, ove: \(x^2+1,5^x\)). Umjesto toga, uzmimo \(\cos⁡x\) iz zagrada.
\(\cos⁡x (2\cos⁡x-2\sin⁡x)=0\)	"Razdvojimo" jednadžbu na dvije.
\(\cos⁡x=0\); \(2\cos⁡x-2\sin⁡x=0\)	Riješimo prvu jednadžbu pomoću brojčane kružnice. Podijelimo drugu jednadžbu s \(2\) i pomaknimo \(\sin⁡x\) na desnu stranu.
\(x=±\)\(\frac(π)(2)\) \(+2πk\), \(k∈Z\). \(\cos⁡x=\sin⁡x\)	Dobiveni korijeni nisu uključeni u ODZ. Stoga ih nećemo pisati u odgovoru. Druga jednadžba je tipična. Podijelimo to s \(\sin⁡x\) (\(\sin⁡x=0\) ne može biti rješenje jednadžbe jer u ovom slučaju \(\cos⁡x=1\) ili \(\cos⁡ x=-1\)).
	Ponovno koristimo krug.
\(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\)	Ove korijene ne isključuje ODZ, pa ih možete napisati u odgovoru.

Odgovor: \(x=\)\(\frac(π)(4)\) \(+πn\), \(n∈Z\).

cos jednadžba x = A

Svaki korijen jednadžbe

cos x = A (1)

može se smatrati apscisom neke sjecišne točke sinusoide y = cosx s ravnom linijom y =A , i obrnuto, apscisa svake takve sjecišne točke jedan je od korijena jednadžbe (1). Dakle, skup svih korijena jednadžbe (1) podudara se sa skupom apscisa svih sjecišnih točaka kosinusnog vala y = cosx s ravnom linijom y = A .

Ako | A| >1 , zatim kosinus y = cosx ne siječe s linijom y = A .

U ovom slučaju jednadžba (1) nema korijena.

Na |A| < 1 postoji beskonačno mnogo točaka sjecišta.

za a > 0

za< 0.

Sve te sjecišne točke podijelit ćemo u dvije skupine:

A -2 , A - 1 , A 1 , A 2 , ... ,

B -2 , B - 1 , B 1 , B 2 , ... ,

Točka A ima apscisu arccos A , a sve ostale točke prve skupine odvojene su od nje na udaljenostima umnošcima 2 π

arccos a+ 2k π . (2)

Točka U, kao što se lako može razumjeti iz slika, ima apscisu - arccosA , a sve ostale točke druge skupine udaljene su od nje na udaljenostima koje su višekratnike 2 π . Stoga su njihove apscise izražene kao

arccos A+ 2nπ . (3)

Dakle, jednadžba (1) ima dvije skupine korijena definirane formulama (2) i (3). Ali ove dvije formule očito se mogu napisati kao jedna formula

x = ± arccos a+ 2m π , (4)

Gdje m prolazi kroz sve cijele brojeve (m = 0, ±1, ±2, ±3, ...).

Rezoniranje koje smo proveli pri izvođenju ove formule ispravno je samo ako
| a| =/= 1. Međutim, formalno relacija (4) određuje sve korijene jednadžbe cosx=a i na | A| =1. (Dokaži!) Stoga možemo reći da formula (4) daje sve korijene jednadžbe (1) za bilo koje vrijednosti A , Samo ako |A| < 1 .

Ali ipak u tri posebna slučaja ( A = 0, A = -1, A= +1) preporučamo da ne koristite formulu (4) , ali koristite druge relacije. Korisno je zapamtiti da su korijeni jednadžbe cos x = 0 dati su formulom

x = π / 2 +n π ; (5)

korijeni jednadžbe cos x = -1 dati su formulom

x = π + 2m π ; (6)

i konačno, korijeni jednadžbe cos x = 1 dati su formulom

x = 2m π ; (7)

Zaključno napominjemo da formule (4) , (5), (6) i (7) točni su samo pod pretpostavkom da je željeni kut x izraženo u radijanima. Ako je izraženo u stupnjevima, tada je potrebno te formule prirodno promijeniti. Dakle, formula (4) treba zamijeniti formulom

x = ± arccos a+ 360° n,

formula (5) formula

x = 90° + 180° n itd.